Is it statistically wrong to adjust for sex and race then do subgroup based on them?

Question

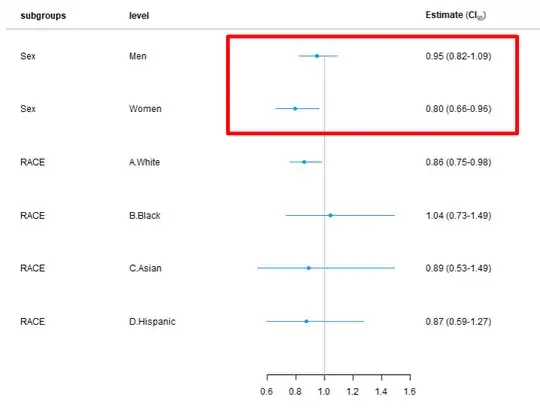
I am doing for subgroup analysis of early mortality (Outcome) based on Transfusion(WITH ADJUSTMENT for both Sex and RACE), I got the results showing that transfusion is associated with higher mortality, while in the un-adjusted model (after EXCLUSION of Sex and race from the adjustment) and doing subgroup based on sex and race, I got more reasonable results (shown below: Transfusion is associated with less risk of mortality). I added collinearity results using vif and no-collinearity exist. I need to know why the results flipped with adjustment as it doesn't make any clinical sense to get lower mortality in the entire cohort and higher mortality in each subgroup of sex.

Is it statistically wrong to adjust for sex and race then do subgroup based on them?

########## Figure 1. The HR < 1 for transfusion (un-adjusted), so I am wondering why HR > 1 after adjusting for sex and race
library(Publish)
Publish::publish(E<-glm(Outcome ~   Transfusion, family = "binomial", data =di ),digits = 3)
# Variable Units OddsRatio         CI.95  p-value 
# Transfusion     0       Ref                        
#                 1     0.880 [0.786;0.985]   0.0263 
sub_log <- subgroupAnalysis(E,di,treatment="Transfusion",
                            subgroups=~Sex+ RACE, factor.reference="inline"); sub_log  ;plot(sub_log)
########## Figure 2. The HR > 1 after adjusting for sex and race for transfusion vs no transfusion in each subgroup
Publish::publish(E<-glm(Outcome ~  Sex+ RACE + Transfusion, family = "binomial", data =di ),digits = 3); car::vif(E)
sub_log <- subgroupAnalysis(E,di,treatment="Transfusion",
                            subgroups=~Sex+ RACE, factor.reference="inline"); sub_log  ;plot(sub_log)
##########  Figure 3.The details of my dataframe (big data)
table(di$Sex, di$RACE, di$Outcome, di$Transfusion)

Figure 1. The HR < 1 for transfusion, so I am wondering why HR > 1 after adjusting for sex and race

Figure 2. The HR > 1 after adjusting for sex and race for transfusion vs no transfusion in each subgroup

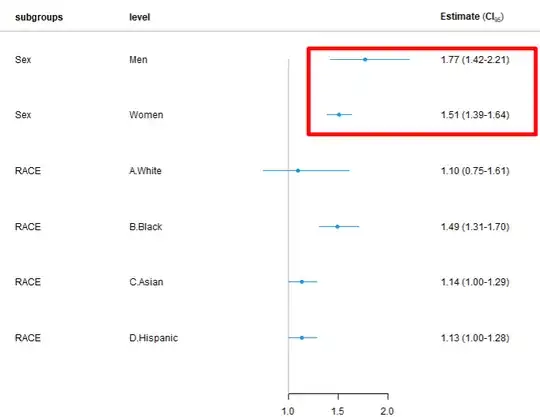
Figure 3. The details of my dataframe (big data) is as follow

Edits I am adding the results of logistic regression after adding interaction term based on @Robert.Long's precious input that is showing a higher mortality among women without statistical difference based on transfusion. I believe that the use of subgroup analysis is essential if we want to show the odds ratio of transfusion in each sex subset with adjustment considering acknowledgement of the limitations.

Answer 1

I wouldn't say that it is "statistically wrong". However I would say that, in general, it is bad practice due to a considerable loss of statistical power in subgroup analyses.

Key Considerations

1. Pre-planning: Pre-planned analyses enable you to determine sample sizes via power calculations. Subgroup analysis, especially when performed post hoc, often lacks sufficient statistical power due to smaller sample sizes in each subgroup.

2. Alternative Approach: Instead of stratifying the data, I would strongly suggest modelling sex and RACE directly by by including interactions. This approach avoids the loss of power associated with subgroup analyses, while enabling you to evaluate effect modification.

   By doing so, the model allows the full dataset to contribute to the analysis: $$ Y = \beta_0 + \beta_1 \text{Transfusion} + \beta_2 \text{sex} + \beta_3 \text{RACE} + \beta_4 (\text{Transfusion} \times \text{sex}) + \beta_5 (\text{Transfusion} \times \text{RACE}) + \epsilon $$ Here, $\beta_4$ and $\beta_5$ capture the effect modification by sex and RACE, respectively.

3. Implementation: Using R, the model can be implemented as:

   Outcome ~ Transfusion + sex + RACE + Transfusion:sex + Transfusion:RACE
   

The interaction terms (Transfusion:sex and Transfusion:RACE) will indicate whether the effect of Transfusion differs by sex or RACE.

Why This is Better:

• Power: Interaction modelling uses the entire dataset, improving the ability to detect effects compared to separate subgroup analyses.
• Confidence Intervals: Interaction terms yield narrower confidence intervals due to larger effective sample sizes.
• Multiple Testing: Subgroup analyses often involve multiple comparisons, increasing the risk of type I errors. Interaction modelling helps to avoid this pitfall by testing heterogeneity directly.

Summing Up

While subgroup analyses are not inherently incorrect, they often result in diminished statistical power and broader confidence intervals. Modelling interactions is a more statistically robust alternative that maintains power while evaluating effect modification.

For highly relevant further reading, I highly recommend Regression Modelling Strategies book by Frank Harrell$^\dagger$,and the Consolidated Standards of Reporting Trials (CONSORT) 2010 Statement, a set of evidence-based recommendations designed to improve the transparency and quality of reporting in randomised controlled trial. Authored by an international group of researchers, trialists, methodologists, and journal editors, this explains the rationale behind each checklist item in the CONSORT Statement and provides illustrative examples of both good and bad reporting of RCTs. Its goal is to help authors, reviewers, and editors ensure RCT reports are complete, allowing for critical appraisal and replication.

$^\dagger$ Regression Modeling Strategies is an absolutely amazing textbook, which is essential reading for anyone doing regression analysis. Also, Frank is a regular contributor over at Cross Validated. I regularly read his latest contributions over there, and have learned so much over the years from doing so. His blog and main website are also fantastic.

References

Harrell, Jr, F. E., & Harrell, F. E. (2015). Multivariable modeling strategies. Regression Modeling Strategies: With applications to linear models, logistic and ordinal regression, and survival analysis, 63-102. https://link.springer.com/book/10.1007/978-3-319-19425-7

Moher, D., Hopewell, S., Schulz, K. F., Montori, V., Gøtzsche, P. C., Devereaux, P. J., ... & Altman, D. G. (2010). CONSORT 2010 explanation and elaboration: updated guidelines for reporting parallel group randomised trials. Bmj, 340.
https://www.bmj.com/content/bmj/340/bmj.c869.full.pdf