When the regression models outperforms naive method?

Question

I followed from this question.

---

Case1:

I have the following task to do: Training by the consecutive 3 days to predict the each 4th day. Each day data represents one CSV file which has dimension 24x25. Every datapoints of each CSV file are pixels.

Now, I need to do that, predict day4(means 4th day) by using training data day1, day2, day3(means three consecutive days), after then calculate mse between predicted day4 data and original day4 data. Let's call it mse1.

Similarly, I need to predict the day5 (means 5th day) by using training data day2, day3, day4, and then calculate the mse2(mse between predicted day5 data and original day5 data)

I need to predict day6(means 6th day)by using training data day3, day4, day5, and then calculate mse3(mse between predicted day6 data and original day6)

..........

And finally I want to Predict day93 by using training data day90, day91, day92,calculate mse90(mse between predicted day93 data and original day93)

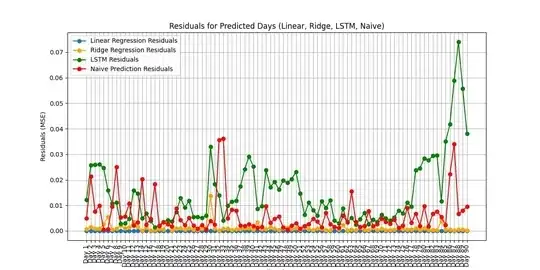
I want to use in this case Ridge regression, Linear regression and LSTM model. And we have 90 mse for each model.

Case2:

Here I am using, is known as "the" naive forecast, or a "random walk" forecast. It is often hard to beat.

Naive approach is:

The guess for any day is simply the map of the previous day. I mean simply guess that day2 is the same as day1, guess that day3 is same as day2, guess that day4 is same as day3,....., guess that day91 is same as day90. I mean Predict next day's data using current day's data(predicted_data = current_day_data). Then calculate mse between next_day_data and current_day_data.

Results:

• In case1, I observe that, It is extremely common for very simple methods(regression models) to outperform complex ones(lstm) in low data situations. This is satisfying as expected. Simple methods will be especially competitive in low data situations. "Competitive" quite simply means "lower prediction error".

• In case2, we know naive method often very hard to beat, means lower MSE, but it is outperformed by simple regression approach in case1.

My questions:

• In which situation would one simple regression model(in case1) outperform a naive method (in case2)? I mean, how to know specifically why one simple method outperforms another naive one on my specific dataset?

• how to dig my data set to understand one simple method outperforms another?

My data sample for example the day1,day2,day3,day4.

Answer 1

This is going to depend very much on the data. Methods other than a purely naive approach (eg., last one carried forward as mentioned in the OP), should outperform the naive method for a number of reasons. Some of those are:

• When the data exhibits a deterministic trend
• When there are patterns in the data such as seasonality
• When there is a dependence on covariates.

Simple regression models often do not do very well with time series data because the assumption of independent and identically distributed data is usually violated. However, there are classes of regression model such as mixed effects models that model the residual covariance matrix using, for example, AR(1), Toeplitz or fully unstructured, which could be expected to out-perform naive methods. For further reading about modelling the residual covariance matrix, this may be of some use:

Beyond AR(1) as a covariance structure for mixed models with repeated measures

Time series methods such as ARIMA would also be expected to outperform the naive methods.

More sophisticated machine-learning methods such as LSTM, as mentioned in the question, could also be considered.