How bootstrapping works for prediction intervals?

Question

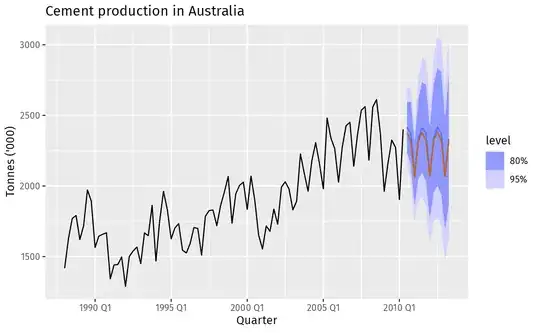
I'm experimenting with prediction interval (PI) over univariant time-data using skforecast pythonic package..

in the documentation it is mentioned that:

Prediction intervals

A prediction interval defines the interval within which the true value of the target variable can be expected to be found with a given probability. Rob J Hyndman and George Athanasopoulos, in their book Forecasting: Principles and Practice, list multiple ways to estimate prediction intervals, most of which require that the residuals (errors) of the model to be normally distributed. If this cannot be assumed, one can resort to bootstrapping, which requires only that the residuals be uncorrelated. This is one of the methods available in skforecast. A more detailed explanation of prediction intervals can be found in the Probabilistic forecasting: prediction intervals and prediction distribution user guide.

in user guide I found helpful info about bootstrapping method works based on $y_t=\hat{y}_{t \mid t-1}+\epsilon_1$ and prediction intervals can be computed by:

calculating the $\alpha / 2$ and $1-\alpha / 2$ percentiles at each forecasting horizon

but still, I can't figure out:

1. Why are the PI outputs (gray lines) so different for certain setups like the below?

# Predict intervals for the next 7 steps, quantiles 10th and 90th
# ==============================================================================
predictions = forecaster.predict_interval(
steps               = 7,
n_boot              = 10,           # iterations
interval            = [10, 90],     # quantiles 10th and 90th [80% interval]
random_state        = 123,          # for reproducibility
...
)

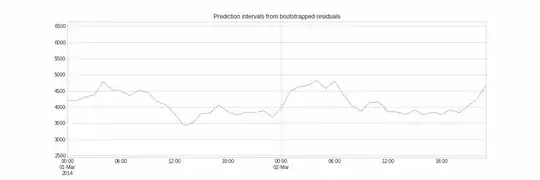
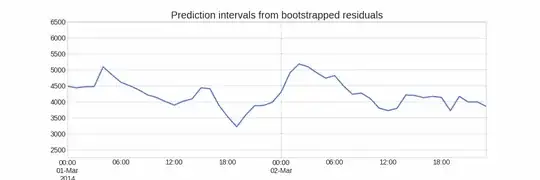
Based on the picture in userguide:

2. How final PI output (pink interval) is computed out of the rest of Bootstrapped PIs?:

Fig. 1: Diagram of how to create prediction intervals using bootstrapping. ref	Fig. 2: PI for Bootstrapping residuals. ref

---

3. why PI distribution per step is so different? Distribution for 1st step is low width and the last one is so wider! Distribution-wisely I found a similar post

# Ridge plot of bootstrapping predictions
# ==============================================================================
_ = plot_prediction_distribution(boot_predictions, figsize=(7, 4))

---

Related materials found:

• p-value vs. confidence interval obtained in Bootstrapping
• Explaining to laypeople why bootstrapping works

Answer 1

1. Why are the PI outputs (gray lines) so different for certain setups like the below?

You've astutely observed that the PI outputs (represented by the gray lines) can vary significantly depending on the specific model setup and data characteristics. Several key factors influence this variability:

• Model Uncertainty: The inherent uncertainty of the model directly impacts the width of the PIs. Higher model uncertainty generally leads to wider intervals.

• Data Variability: The more variability present in your data, the wider the PIs tend to be. The model needs to account for a broader range of possible outcomes.

• Bootstrapping Iterations: The number of bootstrapping iterations specified by n_boot plays a crucial role. Using only ten iterations might not be sufficient to capture the full spectrum of uncertainty. Consider increasing this value to stabilize the PIs.

• Quantile Choice: The specific quantiles selected (10th and 90th percentiles in your case) affect the width of the PIs. Opting for wider intervals, such as the 5th and 95th percentiles, will naturally result in broader PIs.

---

2. How final PI output (pink interval) is computed out of the rest of Bootstrapped PIs?

Computation of the Final PI:

The final PI output (represented by the pink interval in your reference image) is typically computed by aggregating the PIs generated from each bootstrapping iteration. Here's how the process usually works:

• You have a set of bootstrapped predictions at each forecasting step. For example, you might have 100 bootstrapped predictions per step. The desired percentiles are calculated from these predictions independently for each step. For a 95% PI, you would compute the 2.5th and 97.5th percentiles.

• The final PI for each step is then represented by the lower and upper percentiles obtained in the previous step.

This aggregation process allows you to construct the final PI by leveraging the information from all the bootstrapped iterations. Increasing PI Width over the Forecasting Horizon The observation that the PI distribution widens as you move further into the future is a natural consequence of increasing uncertainty. This phenomenon can be attributed to several factors:

• Limited Information: As the model makes predictions further away from the last observed data point, it has less reliable information to work with. The further into the future you go, the more the model has to rely on its own predictions rather than actual data.

• Error Propagation: Any errors or uncertainties in the model's predictions at earlier steps will propagate and accumulate as you move forward in time. This compounding effect leads to broader PI distributions for later forecasting horizons.

• Increasing Plausible Range: With each additional step into the future, the range of plausible values for the target variable expands. The model needs to account for a broader set of possible outcomes, resulting in wider PIs.

In summary, the variability in PI outputs, the computation of the final PI, and the increasing PI width over the forecasting horizon are all inherent characteristics of the bootstrapping approach used in skforecast. Understanding these nuances is crucial for interpreting and effectively utilizing prediction intervals in your time-series forecasting tasks.

Answer 2

1. Why are the PI outputs (gray lines) so different for certain setups like the below?

As it is mentioned in the addressed referenced book by R. J Hyndman & G. Athanasopoulos in skforecast documentation, gray lines are:

“blocked bootstrap”, where contiguous sections of the time series are selected at random and joined together.

However, the estimated parameters will be different, so the forecasts will be different even if the selected model is the same. This is a time-consuming process as there are a large number of series.

Bootstrapped time series is used to improve forecast accuracy.

Note: A similar technique is used in Ensemble Learning in random forest algorithm as a : :

Bootstrap - Allow Bootstrapped Sampling for each training subset of the feature

:

• ✍️ Definition - Random sampling with replacement
• ✍️ it bootstraps a selection of rows for each split.
• This means that the trees are trained on a subset of features and a subset of rows of data. As a result, the trees are very different from each other

see the details in this workaround

---

2. How final PI output (pink interval) is computed out of the rest of the Bootstrapped PIs?

based on documentation using : Bagged forecasts

If we produce forecasts from each of the additional time series, and average the resulting forecasts, we get better forecasts than if we simply forecast the original time series directly. This is called “bagging” which stands for “bootstrap aggregating”. Finally, we average these forecasts for each time period to obtain the “bagged forecasts” for the original data.

Figure 12.22: Comparing bagged ETS forecasts (the average of 100 bootstrapped forecasts in orange) and ETS applied directly to the data (in blue). ref