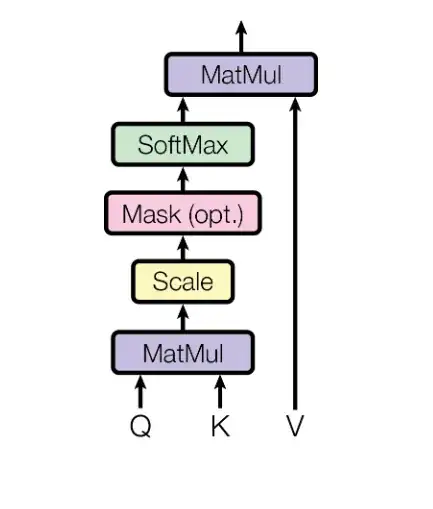
I am trying to understand the reasoning behind the Transformer architecture.
In "Attention is all you need", the weights for the scaled dot-product attention is defined as the scaled dot-product of the keys and values, passed through a SoftMax:
Conceptually, I understand that these weights are used to "select" other tokens to "take context" from their values based on their relevance. Therefore, it makes sense that they should be between 0 and 1.
However, I don't understand why we don't simply use an activation function like the Sigmoid here.
I know that the outputs of Softmax add up to 1. And it seems like the authors try to preserve this property - even when the paper describes masking, they don't simply set the post-softmax weights to 0 (which seems like a more obvious solution, but would make the sum <= 1). Instead, they subtract infinity from the Softmax inputs, which makes sure that the weights still sum up to 1.
Why is it so important that these weights add up to 1? In my understanding, this is usually used for values that represent probabilities. However, these weights don't represent probabilities, right? They are simply scores of how "relevant" the other tokens are to the context of the current tokens. Therefore, it would make sense to me if a similar model learned attention weights that sum up to more than 1.
Is my intuition for the "meaning" of these values correct? Is there a reason why it is beneficial to have the attention weights sum up to 1? Has there been any research on alternative options? Or is the use of Softmax here arbitrary? Would a simple activation function work here instead of Softmax?