How could I estimate slope of lines on a scatter plot?

Question

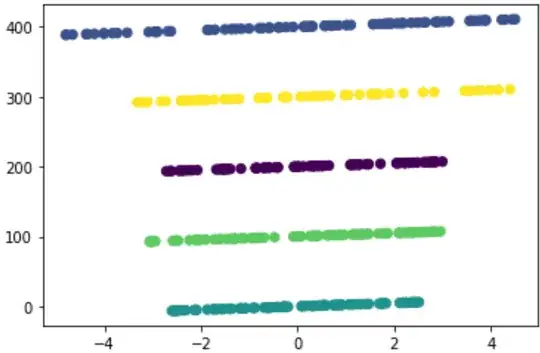
I have a list of coordinate pairs. To the human eye, they form lines with a constant slope:

This is how I generated that image above:

import numpy as np
np.random.seed(42)
slope = 1.2 # all lines have the same slope
offsets = np.arange(10) # we will have 10 lines, each with different y-intercept
xslist=[]
yslist=[]
for offset in offsets:
    # each line will be described by a variable number of points:
    size = np.random.randint(low=50,high=100)
 # eachline starts from somewhere -5 and -2 and ends between 2 and 5
xs = np.random.uniform(low=np.random.uniform(-5,-2), high=np.random.uniform(2,5),size=size)

 # add some random offset and some random noise
ys = slope * xs + offset + np.random.normal(loc=0, scale=0.1, size=1) + np.random.normal(loc=0, scale=0.01, size=size)
xslist.append(xs)
yslist.append(ys)


bring all x and y points together to single arrays
xs = np.concatenate(xslist) # xs: array([-0.37261674,  0.58267626, -3.72592914 ...
ys = np.concatenate(yslist) # ys: array([-0.53638699,  0.61729781, -4.52132114,
plot results
import matplotlib.pyplot as plt
plt.scatter(xs,ys)

I can generate lots of xs and ys. In my real world scenario, I won't know which point belongs to which line, so cannot simply separate the points to different groups and just apply least squares fitting to each group.

How could I, using machine learning or otherwise, build a function which takes xs and ys as input, and returns a slope estimate of the lines on an image like above?

Why simple least squares fitting doesn't seem to work

Let's generate new data where the failure of least squares fitting is more obvious. Let's have a slope of 2.4 and y-intercepts between 0 and a few hundred.

Data generation:

import numpy as np
np.random.seed(42)
slope = 2.4
offsets = np.arange(0,500,100)
xslist=[]
yslist=[]
for offset in offsets:
size = np.random.randint(low=50,high=100)

xs = np.random.uniform(low=np.random.uniform(-5,-2), high=np.random.uniform(2,5),size=size)
ys = slope * xs + offset + np.random.normal(loc=0, scale=0.1, size=1) + np.random.normal(loc=0, scale=0.01, size=size)

xslist.append(xs)
yslist.append(ys)


xs = np.concatenate(xslist)
ys = np.concatenate(yslist)

Least squares fitting of a line using np.polyfit():

a, b = np.polyfit(xs, ys, deg=1)

Note that I cannot fit to just one line, as I don't know which points belong to one line.

Plot results:

import matplotlib.pyplot as plt
plt.figure(figsize=(10,10))
plt.scatter(xs,ys)
line_x = np.arange(-5,5,0.01)
line_y = a*line_x + b
plt.plot(line_x,line_y,c='r',linewidth=10)
plt.gca().set_aspect(1/8)

ie:

The obtained slope using least squares fitting (ie the slope of the red line) is very much different than the slope of the lines formed by black dots. (Note that the scale is different on the x and y axis.)

Printing both a (our slope estamate) and the real slope slope:

print(a)
print(slope)

get:

4.295790412452058
2.4

This error is too much for my real world application.

Function to generate mock data

As requested in the comments, here is a function to generate data similar to the above examples:

def get_data(number_of_examples):
np.random.seed(42)

list_of_xs = []
list_of_ys = []
true_slopes = []

for _ in range(number_of_examples):

    slope = np.random.uniform(low=-10, high=10)

    offsets = np.arange(0,
                        np.random.randint(low=20, high=200),
                        np.random.randint(low=1, high=10))
    xslist=[]
    yslist=[]

    for offset in offsets:

        size = np.random.randint(low=np.random.randint(low=40, high=60),
                                 high=np.random.randint(low=80, high=100))

        xs = np.random.uniform(low=np.random.uniform(-5,-2),
                               high=np.random.uniform(2,5),size=size)
        ys = slope * xs + offset + \
            np.random.normal(loc=0, scale=0.1, size=1) + \
            np.random.normal(loc=0, scale=0.01, size=size)

        xslist.append(xs)
        yslist.append(ys)

    xs = np.concatenate(xslist)
    ys = np.concatenate(yslist)

    list_of_xs.append(xs)
    list_of_ys.append(ys)
    true_slopes.append(slope)

return list_of_xs, list_of_ys, true_slopes

Try it, get 10 examples:

list_of_xs, list_of_ys, true_slopes = data = get_data(10)

Plot results (the slope of the red line is what I am trying to predict using the coordinates of the blue dots):

for xs, ys, true_slope in zip(list_of_xs, list_of_ys, true_slopes):
    plt.figure()
    plt.scatter(xs, ys)
    plt.plot(xs, xs*true_slope, c='r')

and so on.

score 9 · Accepted Answer · answered Dec 29 '21 at 19:26

The procedure that you can use is the following. First cluster your data with gaussian mixture models. This method should also work with multiple lines with different slopes. It should be able to deal with intersections as points near an intersection can belong to both clusters and a wrong classification will not lead to huge differences in the results of the regression.

I will post the complete code.

# Your code for generating the data
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
slope = 2.4
offsets = np.arange(0,500,100)
xslist=[]
yslist=[]
for offset in offsets:
size = np.random.randint(low=50,high=100)

xs = np.random.uniform(low=np.random.uniform(-5,-2), high=np.random.uniform(2,5),size=size)
ys = slope * xs + offset + np.random.normal(loc=0, scale=0.1, size=1) + np.random.normal(loc=0, scale=0.01, size=size)

xslist.append(xs)
yslist.append(ys)


xs = np.concatenate(xslist)
ys = np.concatenate(yslist)

We will use your data points to generate multiple gaussian mixture models. We will fix the number of components by using the number of components with the minimal value of the Bayesian Information Criterion (BIC).

# Create multiple Gaussian Mixture models
from sklearn.mixture import GaussianMixture
X = np.vstack((xs, ys)).T
n_components = np.arange(1, 21)
models = [GaussianMixture(n, covariance_type='full', random_state=0).fit(X) for n in n_components]
Get optimal number of components by using the index of the components with the minimal value for the Bayesian Information Criterion (BIC)
n_components_optimal = np.argmin(np.array([model.bic(X) for model in models])) + 1

Plot the results and see how well the clustering with the optimal number of clusters works.

# Code for plotting
gaussian_mixture_model_optimal = GaussianMixture(n_components_optimal, covariance_type='full', random_state=0).fit(X)
labels = gaussian_mixture_model_optimal.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis')

Now, use the clustered data and create subdataframes from them and fit your linear regressions.

import pandas as pd
df = pd.DataFrame({
    "x": xs,
    "y": ys,
    "cluster": labels,
})

cluster_number = 1
X_sub = df.query('cluster == @cluster_number').values

How could I estimate slope of lines on a scatter plot?

bring all x and y points together to single arrays

plot results

Why simple least squares fitting doesn't seem to work

Function to generate mock data

1 Answers1

Get optimal number of components by using the index of the components with the minimal value for the Bayesian Information Criterion (BIC)