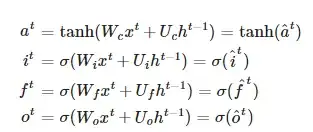Number of parameters in an LSTM model

Question

How many parameters does a single stacked LSTM have? The number of parameters imposes a lower bound on the number of training examples required and also influences the training time. Hence knowing the number of parameters is useful for training models using LSTMs.

Answer 1

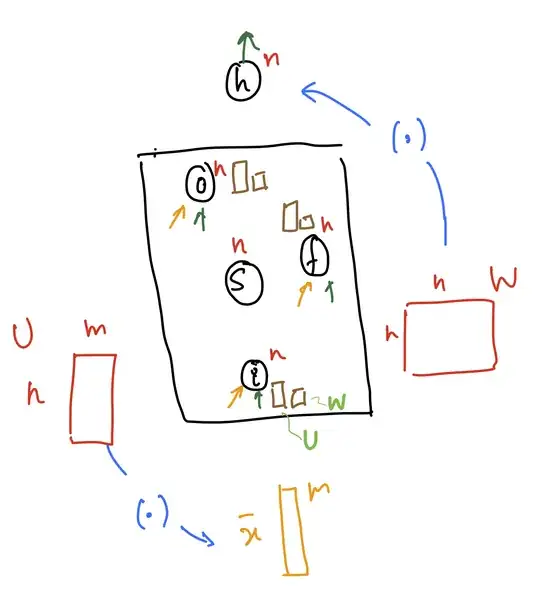
The LSTM has a set of 2 matrices: U and W for each of the (3) gates. The (.) in the diagram indicates multiplication of these matrices with the input $x$ and output $h$.

• U has dimensions $n \times m$
• W has dimensions $n \times n$
• there is a different set of these matrices for each of the three gates(like $U_{forget}$ for the forget gate etc.)
• there is another set of these matrices for updating the cell state S
• on top of the mentioned matrices, you need to count the biases (not in the picture)

Hence total # parameters = $4(nm+n^{2} + n)$

Answer 2

Following previous answers, The number of parameters of LSTM, taking input vectors of size $m$ and giving output vectors of size $n$ is:

$$4(nm+n^2)$$

However in case your LSTM includes bias vectors, (this is the default in keras for example), the number becomes:

$$4(nm+n^2 + n)$$

Answer 3

According to this:

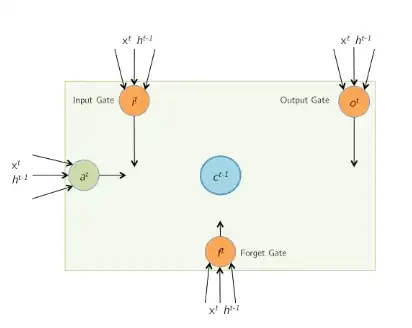
LSTM cell structure

LSTM equations

Ingoring non-linearities

If the input x_t is of size n×1, and there are d memory cells, then the size of each of W∗ and U∗ is d×n, and d×d resp. The size of W will then be 4d×(n+d). Note that each one of the dd memory cells has its own weights W∗ and U∗, and that the only time memory cell values are shared with other LSTM units is during the product with U∗.

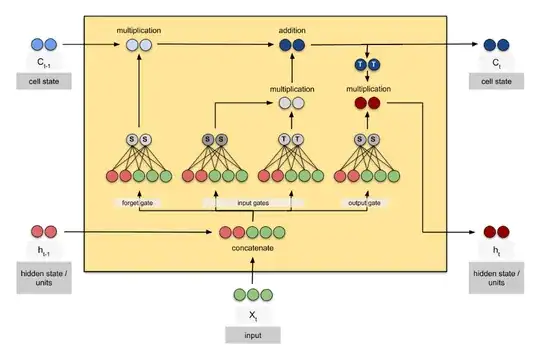
Thanks to Arun Mallya for great presentation.

Answer 4

to completely receive you'r answer and to have a good insight visit : https://towardsdatascience.com/counting-no-of-parameters-in-deep-learning-models-by-hand-8f1716241889

g, no. of FFNNs in a unit (RNN has 1, GRU has 3, LSTM has 4)

h, size of hidden units

i, dimension/size of input

Since every FFNN(feed forward neural network) has h(h+i) + h parameters, we have

num_params = g × [h(h+i) + h]

Example 2.1: LSTM with 2 hidden units and input dimension 3.

g = 4 (LSTM has 4 FFNNs)

h = 2

i = 3

num_params

= g × [h(h+i) + h]

= 4 × [2(2+3) + 2]

= 48

    input = Input((None, 3))
    lstm = LSTM(2)(input)
    model = Model(input, lstm)

thanks to RAIMI KARIM

Answer 5

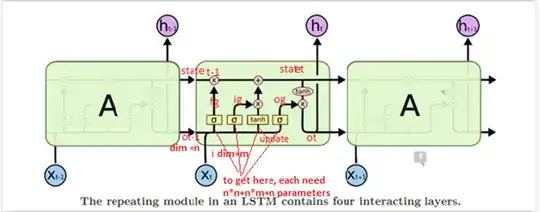
To make it clearer , I annotate the diagram from http://colah.github.io/posts/2015-08-Understanding-LSTMs/.

ot-1 : previous output , dimension , n (to be exact, last dimension's units is n )

i: input , dimension , m

fg: forget gate

ig: input gate

update: update gate

og: output gate

Since at each gate, the dimension is n, so for ot-1 and i to get to each gate by matrix multiplication(dot product), need nn+mn parameters, plus n bias .so total is 4(nn+mn+n).