Compare each array $i$ member to all array $j$ member where $(i > j)$ , in time less than $O(n^2)$

Question

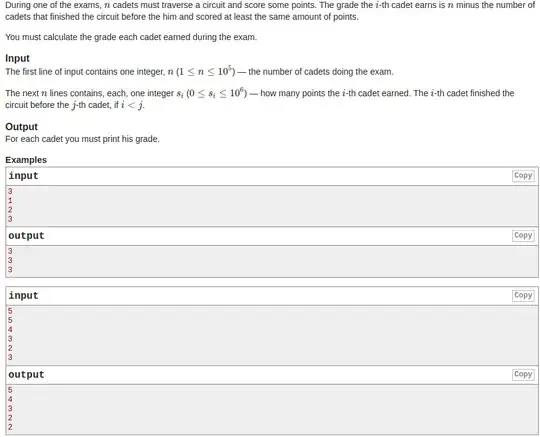
I am new to algorithms so sorry to ask simple question

I am working on a problem which is about array of integers, my solution is right but not good enough, because I have time exceeded exception on codeforces. I think solution where solution's time < O(n^2) would be right.

My solution:

int n;
cin >> n;

int currentScore = n;
int credits[n];
int grades[n];
for (int i = 0; i < n; i++) {
    cin >> credits[i];
    for (int j = 0; j < i; j++) {
        if (credits[i] <= credits[j]) {
            currentScore--;
        }
    }
    grades[i] = currentScore;
    currentScore = n;
}

for (int i = 0; i < n; i++) {
    cout << grades[i] << endl;
}

return 0;

Answer 1

Create a binary tree containing the points, either each node also containing the number of elements in each sub tree . For each candidate, determine the number of candidates arriving earlier, and having same or higher score using the tree, then add the candidates score to the tree.

Should work in O(n log n). I doubt O(n) is possible.

PS chi’s answer is a lot easier, and you probably have a library for the sorting, which is the hard part.

Answer 2

A basic approach would be as follows.

Given input $a_1,a_2,\ldots$ we build an array of pairs $A=(1,a_1),(2,a_2),\ldots$.

Now, in $O(n\log n)$ time, we can sort it according to the second component of each pair.

When $A$ is sorted in such way, it's easy to compute the score and modify $A$ so that it becomes of the form $A=(i,{\sf score}_i),(j,{\sf score}_j),\ldots$. This should cost $O(n)$.

Now, we can sort $A$ once more, according to the first component of each pair, so that we have $A=(1,{\sf score}_1),(2,{\sf score}_2),\ldots$. This costs $O(n\log n)$.

Finally, we print the scores.