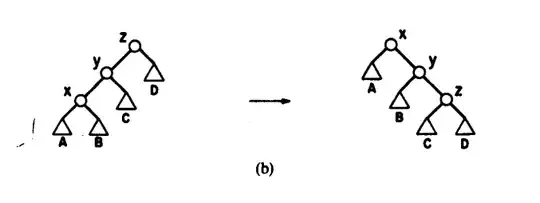
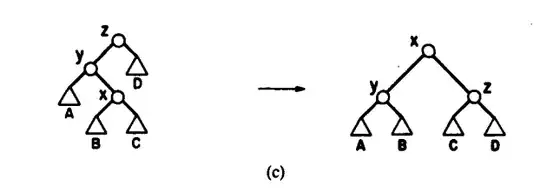
The original paper describing splay trees Self-Adjusting Binary Search Trees by Sleator and Tarjan claims that:
Splaying not only moves x to the root, but roughly halves the depth of every node along the access path.
What is the intuition for this claim? The paper includes some figures (splaying in a tree of all zig-zigs or all zig-zags) and while I can see at a high level that splaying helps other parts of the tree, it's not really clear to me where the halving comes from?