This solution assumes all weights are non-negative.
Lemma. There exists an optimal traverse with the following shape ($A, B,C$ may be the same vertex and may coincide with $S,M,T$), where each arrow represents a simple path, and paths represented by different arrows are edge-disjoint.
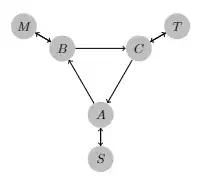
The strict proof of this lemma is somewhat tedious, so I omit it here (the idea is shown in another answer). If I have time in the future, I'll add it into this answer.
Let $d_a(x,y), d_{a+b}(x,y)$ respectively denote the shortest distance between vertexes $x$ and $y$ when edges have weights $a_i$'s and when edges have weights $(a_i+b_i)$'s. Let $\mathrm{opt}$ denote the value of optimal solution, then by this lemma we have
$$
\begin{align*}
\mathrm{opt}\ge\ & d_a(A, B)+d_a(B,C)+d_a(C,A)\\
&+d_{a+b}(B,M)+d_{a+b}(C,T)+d_{a+b}(A,S).
\end{align*}
$$
On the other hand, following the shortest path (with weights $a_i$'s or $(a_i+b_i)$'s accordingly) from $S$ to $A$, then from $A$ to $B$, and so on, constitutes a valid traverse. Easy to see the cost of this traverse is no more than
$$
\begin{align*}
d_a(A, B)+d_a(B,C)+d_a(C,A)+d_{a+b}(B,M)+d_{a+b}(C,T)+d_{a+b}(A,S),
\end{align*}
$$
so
$$
\begin{align*}
\mathrm{opt}\le\ & d_a(A, B)+d_a(B,C)+d_a(C,A)\\
&+d_{a+b}(B,M)+d_{a+b}(C,T)+d_{a+b}(A,S).
\end{align*}
$$
As a result,
$$
\begin{align*}
\mathrm{opt}=\ & d_a(A, B)+d_a(B,C)+d_a(C,A)\\
&+d_{a+b}(B,M)+d_{a+b}(C,T)+d_{a+b}(A,S).
\end{align*}
$$
So one can pre-compute the all-pair shortest paths using Floyd–Warshall algorithm, then exhaust all posible $(A,B,C)$'s to find $\mathrm{opt}$. This algorithm costs $O(N^3)$.
