4

Scenario

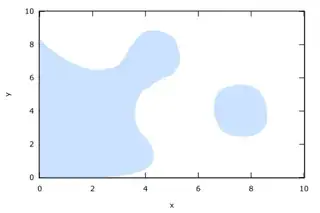
Consider one or more curved shapes in 2D space, clipped to a rectangular viewport. For example:

original

Unfortunately, data that would describe these shapes precisely, is not available.

Input data

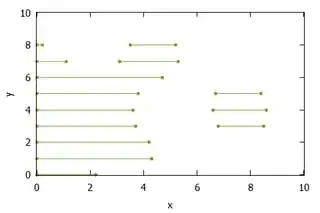
All that is available are the intersections of the shapes with a few horizonal and vertical lines, sampled at coarse intervals:

horizonal intervals vertical intervals

In the example at hand, the available data could be expressed like this:

y    x-ranges
-------------------------
 0   0.0 - 2.2
 1   0.0 - 4.3
 2   0.0 - 4.2
 3   0.0 - 3.7, 6.8 - 8.5
 4   0.0 - 3.6, 6.6 - 8.6
 5   0.0 - 3.8, 6.7 - 8.4
 6   0.0 - 4.7
 7   0.0 - 1.1, 3.1 - 5.3
 8   0.0 - 0.2, 3.5 - 5.2
 9   
10   


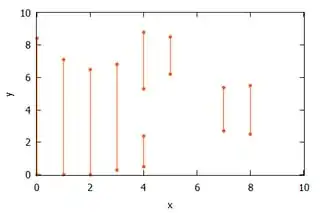
x    y-ranges
-------------------------
 0   0.0 - 8.4
 1   0.0 - 7.1
 2   0.0 - 6.5
 3   0.3 - 6.8
 4   0.5 - 2.4, 5.3 - 8.8
 5   6.2 - 8.5
 6   
 7   2.7 - 5.4
 8   2.5 - 5.5
 9   
10

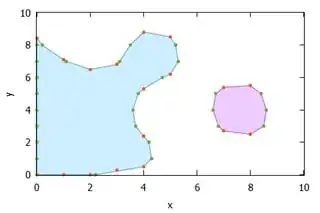
It's not much, but when both sets of intervals are combined, it already allows a human viewer to "see" the original shapes quite well:

all intervals

The Problem

But how would a computer algorithm go about approximating the outlines of the original shapes based on data like this?

Ignoring interpolation/smoothing for now, the problem becomes grouping and ordering the interval end-points in the correct manner to get the ordered vertices of one or more polygons corresponding to the original shapes:

polygons

In the example at hand, the output data of the algorithm could be expressed like this:

Polygon 1:
(0, 0) - (0, 8.4) - (0.2, 8) - (1, 7.1) - (1.1, 7) - (2, 6.5) - (3, 6.8) - (3.1, 7) - (3.5, 8) - (4, 8.8) - (5, 8.5) - (5.2, 8) - (5.3, 7) - (5, 6.2) - (4.7, 6) - (4, 5.3) - (3.8, 5) - (3.6, 4) - (3.7, 3) - (4, 2.4) - (4.2, 2) - (4.3, 1) - (4, 0.5) - (2.2, 0) - (0, 0)

Polygon 2:
(7, 2.7) - (6.8, 3) - (6.6, 4) - (6.7, 5) - (7, 5.4) - (8, 5.5) - (8.4, 5) - (8.6, 4) - (8.5, 3) - (8, 2.5) - (7, 2.7)

Help needed

I'm having trouble coming up with an algorithm to do this. I'd greatly appreaciate:

  • Clarity on what kind of problem this is, what kind of algorithm is needed, etc.
    (Part of what makes this difficult for me is that I don't know what search terms to use to research this.)
  • Pointers to edge cases etc. that I need to consider, that I may not yet have.
  • Pointers to appropriate literature.
  • Suggestions/discussions of the algorithm itself, obviously.
smls
  • 173
  • 4

0 Answers0