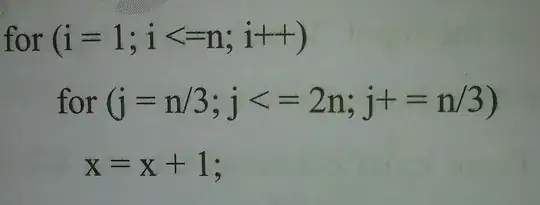What i came up with is this 1) inner loop goes to 2n and at each. step it increments n/3 times threfore 2log n times it will execute 2) outer goes to n incrementing by 1 threfore n times
Hence for each value of outer loop innner executes n* 2log n times... Threfore O(n*2logn)
Que 1) Is this correct
Que2) If it is Correct then how to derive θ(theta), average case.
Please help me here
There are a number of serious misunderstandings in this post.
Assuming that this code takes a pair of starting values $x,n$ as an input, this code describes a function, $f(x,n)$. However, $f$ can be calculated exactly, and there's no reason to describe it in terms of big-O notation. Big-O notation is used to describe an upper bound on a value that you don't know the precise value of. If you're looking to describe the function this code expresses you should calculate it, not use big-O. This code gives the function $f(x,n)=x+6n$.
Even if we ignore 1, I’m having trouble with your calculation. Where did the $\log(n)$ come from? The inner loop executes 6 times, rather than $2\log(n)$ times. I can elaborate on this point if you wish, but you can easily verify this by hand with small numbers.
You cannot leave the $x$ out of an upper bound on the complexity of code if $x$ is a variable in the code that isn't constrained. You might describe this code as $O(x+n)$ but to describe it as $O(n)$ is wrong.
$\Theta$ does not mean the average case complexity. $g=\Theta(f)$ when $g=O(f)$ and $f=O(g)$. Again, you shouldn't describe this using $\Theta$ because we can simply calculate the value exactly.
Despite point $2$, your answer (once we've amended it to be $O(x+n\log(n))$ isn't really wrong (assuming we are caring about an upper bound). This is because it's an upper bound that's bigger than the best description. In this sense, the code is also $O(x+e^{e^n})$. It's just that describing it as such is probably not helpful.
