Why NFA is called Non-deterministic?

Question

I have this [kind of funny] question in mind. Why is the non-deterministic finite automaton called non-deterministic while we define the transitions for inputs. Well, even though there are multiple and epsilon transitions, they are defined which means that the machine is deterministic for those transitions. Which means it's deterministic.

Answer 1

"Deterministic" means "if you put the system in the same situation twice, it is guaranteed to make the same choice both times".

"Non-deterministic" means "not deterministic", or in other words, "if you put the system in the same situation twice, it might or might not make the same choice both times".

A non-deterministic finite automaton (NFA) can have multiple transitions out of a state. This means there are multiple options for what it could do in that situation. It is not forced to always choose the same one; on one input, it might choose the first transition, and on another input it might choose the same transition.

Here you can think of "situation" as "what state the NFA is in, together with what symbol is being read next from the input". Even when both of those are the same, a NFA still might have multiple matching transitions that can be taken out of that state, and it can choose arbitrarily which one to take. In contrast, a DFA only has one matching transition that can be taken in that situation, so it has no choice -- it will always follow the same transition whenever it is in that situation.

Answer 2

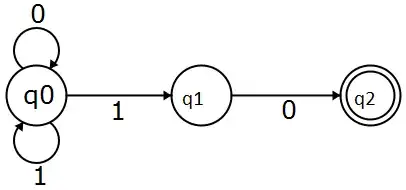
Take this automaton for instance, it's an NFA and it accepts the string $0110$. To be more pedantic, it accepts strings that end in $10$.

To see that we just need to check whether it reaches an accept state.

\begin{align*} q_0 & \rightarrow 1\\ q_0 & \rightarrow 0\\ \color{red}{q_1} &\rightarrow \color{red}{1}\\ q_2 &\rightarrow 0\\ \end{align*}

Now in the red line there was another possibility, that is when reading the second $1$ I could stay in $q_0$ and then stay in $q_0$ when reading the last $0$. Automata have no memory, so there's no way to 'save' a state and check later if my string ends with $10$, it's like this NFA it's making a guess whether the string ends with $10$ before branching to an acceptable state. The nondeterminism here is making lots of choices and always making the right ones.

It's easier to construct an NFA than it is to construct an DFA, the good thing is that both are equivalent.

Answer 3

The transition function of an NFA specifies the allowed transitions at any point in time. There could be more than one option, and the NFA chooses a transition nondeterministically with the goal of eventually reaching an accepting state.

Perhaps you should wait until you learn about nondeterministic Turing machines. Nondeterminism means the same thing in both cases.

Answer 4

Start off with a Finite Automaton. It has states and acceptance states and transitions.

Now, give it more than one trasition rule of of each state, and say that it accepts if there exists a set of transition rules picked after the fact that lead to the acceptance state given an input string.

Once you have your input string, there is a fixed set of concrete transitions and states it goes through (one at a time) to accept that string. But which transitions it picks are only chosen at the end of the string. While the string is being read, which path to take is not determined.

It is non-deterministic. It gets to pick its path through the graph after you give it the entire problem, not as it reads the input.

---

Now, we formalize this differently than this thought experiment, but this gives you motivation why it got that name.

This explains how it got the name in the first place. Yes, you can model NDFA in a completely deterministic way, but names are sticky. Once you have called something Bob, there is a communication cost to renaming it to something else as nobody knows what you are talking about when you call it Alice.

Answer 5

Both DFA and NFA are deterministic in the sense that they will always accept a string that is part of the language they recognize and reject it otherwise. However, when reading a same string repeatedly, i.e. when put in the same initial conditions, not only an NFA may chose different state transitions (and hence different paths, order of paths, etc.) but the exact state in which it ends up may differ as a result.

Consider this NFA, which accepts strings of 0s in multiples of 2 or 3 (borrowed from Sipser's Theory of Computation):

If the input is 0000, the final state will always be the accept state of the upper branch. If it is 000, it will always be the accept state of the lower branch. However, if it is 000000, it can be any of them, depending on the initial choice of branch. A similar situation occurs for rejected strings like 00000.

So the automaton is really non-deterministic in the usual sense of the word, as opposed to its DFA equivalent, in which the final state of the system is unique and predictible for any given string.

Answer 6

Determinism: upon reading the current input letter, there is a single successor state that we move to.

So, upon reading an input word $w$, the future is resolved and is based only on the current state we're in.

Nondeterminism: upon reading the current input letter, there is a subset of candidate successor states that we can move to each.

So, upon reading an input word $w$, the future is not necessarily resolved and we have to guess it.

Answer 7

NFA and DFA are both used to (amongst other things) recognize certain strings.

Non-deterministic finite automaton works like it had an influence on its decisions - it can "choose" to follow a path, or not.

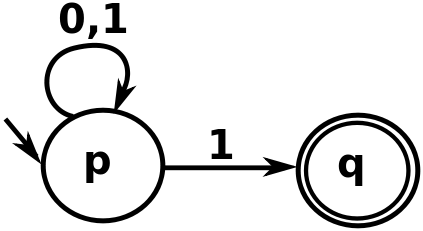
On the image above, when we are dealing with string "00111", notice that when encountering the first "1", there are two possible ways to follow. One can stay at "p" or go to "q". If the automata was to move to the "q", it wouldn't accept the string(since there are no edges coming out of the "q"). But the string can be accepted by this automata by going to the "q" with only the last 1, while staying at "p" for everything else(and that's what's happening).

NFA makes it look like the automata "knew" what is ahead, and chooses accordingly.

Of course it doesn't. DFA and NFA are equivalent in terms of power(you can reduce NFA to DFA and make DFA (probably) simpler with use of NFA), but NFA is useful, because it has allows to define the same languages as DFA while keeping the graphs much shorter and more readable.

There is nothing random in there. The non-deterministic part puts emphasis on the fact that there is some "choice" to take, but the truth is that the automata doesn't take any decisions.

Answer 8

From wikipedia, the best way to think about this is to start with deterministic finite state machines(DFA). For a DFA, each transition is uniquely determined by the current state and the input symbol to be processed. Nondeterministic finite state machines (NFA) are simply what you get when you relax this determinism rule to permit transitions to not be uniquely defined. It's what you get when you remove the determinisim rule from DFAs.

Answer 9

Well here is the mix of some content from book [Introduction to Formal Languages and Automata by Peter Linz 4E] and my understanding.

Consider a game-playing program where the machine needs to make the decision for the next move [say for tic-tac-toe]. Since there are multiple moves possible, we deterministically choose each move and evaluate the move and opt for the best one. Even though the selection process was deterministic and there were many possible moves, the final move made was a single one and was chose as best move while hiding all the tried move-computations from the opponent. [Here we assume that the evaluation process of each possible move was hidden from the opponent].

Hence only one choice was made and opponent is given a illusion such that the move was non-deterministic.

Well if you are not convinced yet by asking that the best move was the product of some deterministic calculations then you must consider the machine which makes perfectly random moves (may be machine looses but it's an NFA).