All references I find about the ANOTHER HAMILTONIAN CIRCUIT problem:
Given a graph and a hamiltonian circuit on it, is there another hamiltonian circuit on it?
I was trying to reduce it to the hamiltonian circuit problem but I always need to add too many or too few circuits to the original one.
Am I going through the good direction? It seems to be very simple...
Edit
Papadimitriou's complexity book refers to its theorem 17.5 for the inspiration for this problem.
I think that a good way for the solution is to consider the graph proposed in Papadimitrious'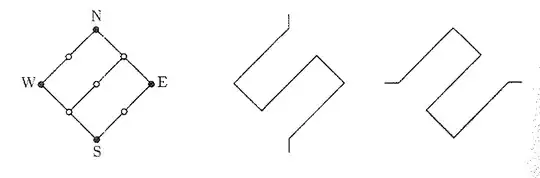
One can for each node of the original graph, transform to the graph shown at the left image. Then, one can connect all these new graphs using the poles N and S and thus obtains a hamiltonian circuit. Then, one uses W and E to connect vertex that were connected in the original graph. In principle, one could connect W with W and E with E.
I only have one more doubt, what happens if the original graph is just a segment, that is, two vertex with a edge between them. My construction would give an extra hamiltonian circuit going from W1->E1->E2->W2->W1 even if the original one didn't have one!
Can you find any other counterexample? This was the solution given in my course and it seems to be partly wrong...