Suppose we have a set of equations like this
p7=f(p1+p6); p6=f(p2+p5); p5=f(p3+p4); p4=f(p3); p3=f(p2); p2=f(p1); p1=f()
It can be represented by computational graph below
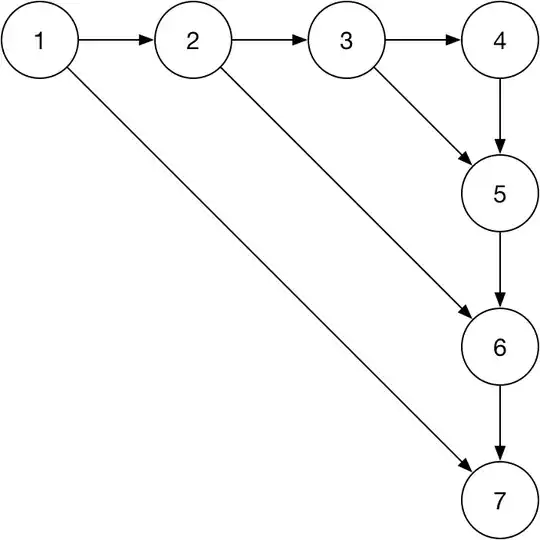
If each intermediate value takes 1 unit of memory, you need at least 4 units to compute p7 without any duplicate computation.
Is there an algorithm for estimating memory needed in this setting for a general DAG?
I found a paper called "Adjoint Dataflow Analysis" for estimating this for restricted set of graphs, but it feels like this ought to be a problem that is covered more generally in graph theory.