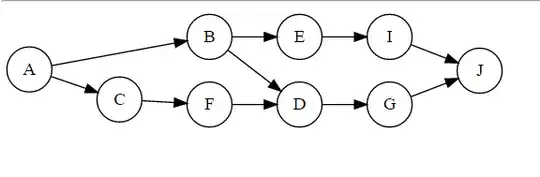
I have a directed graph where all the nodes represent some task that needs to be computed. I need to compute the order of these tasks and also detect any cycles. Running Tarjan's algorithm on the graph gives me both.
To the problem:
I was wondering if there exists a good way to make use of parallelization. For instance, node A goes to node B and C. We can then compute task B and [C,F] in parallel. After that we can compute tasks [E,I] and [D,G] in parallel as well.
What kind of algorithm could detect which subsets of the tasks that can be computed in parallel?
I was thinking about the following procedure:
- Select a start node $n_1$ and a finish node $n_f$.
- Compute all possible paths $n_1 \rightarrow n_f$.
- If there is only one path then this whole branch can be assigned to be computed by one processor.
- Then I mark all nodes on this path.
- Now i select another finishing node and repeat until I have marked all nodes.
- Should there exist more than one path $n_1 \rightarrow n_f$ I reduce the path length by one and instead compute all paths $n_1 \rightarrow n_{f-1}$ where $n_{f-1}$ is a parent to $n_{f}$