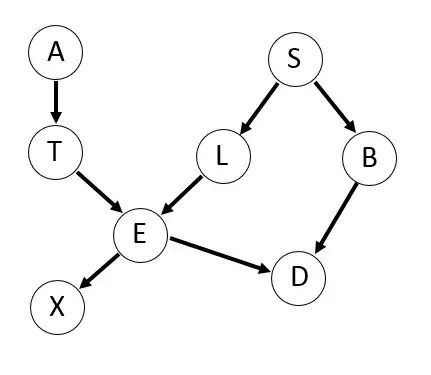
I'm trying to check if my understanding of variable elimination is correct.
Assume the above Bayesian network is factorized as:
$p(a,b,d,e,l,s,t,x) = p(a)p(t|a)p(e|t,l)p(x|e)p(l|s)p(b|s)p(d|b,e)p(s)$
Suppose I want to find $p(e|s)$, this means performing $p(e|s) = \sum_{t,l}p(e|l,t)p(t)p(l|s)$
Now, $p(e|l,t)p(t)= \frac{p(e,l,t)}{p(l,t)}p(t) = \frac{p(e,l,t)}{p(l|t)} = \frac{p(e,l,t)}{p(l)} = p(e,t|l)$. The third equality is due to the unconditioned collider $e$. Marginalizing over $t$ gives us $p(e|l)$.
Subsequently, $p(e|l)p(l|s) = p(e|l,s)p(l|s) = \frac{p(e|l,s)p(s)}{p(s)}p(l|s) = \frac{p(e,l,s)}{p(s)} = p(e,l|s)$, where the first equality is because conditioning on $l$ makes $s$ irrelevant, i.e. $p(e|l,s) = p(e|l)$. And marginalizing over $l$ finally gives $p(e|s)$.
Is this correct?
Also and on to the larger picture, is there a faster way of deriving or 'seeing' this equality? It seems to me that the faster approach is moving the conditioned variables over the conditioning bar, and then marginalizing, that is $\sum_{t,l}p(e|l,t)p(t)p(l|s) = \sum_{t,l}p(e,l,t|s) = p(e|s)$. Is this valid?
Thank you.