3

I'm working on solving the question answered at this page but with different values at the table, my alphabet is {a,b,c} Words that have the same right- and left-associative product

Currently I'm in the stage where I have drawn the DFA of the multiplication table, found its reverse which was an NFA.

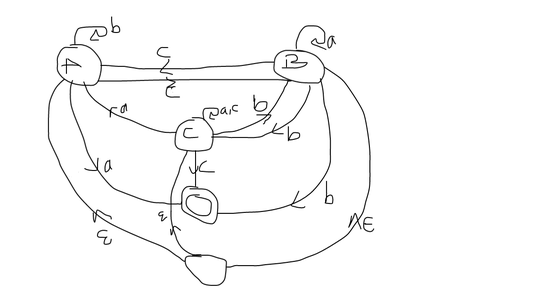
Here is the NFA I got by reversing the multiplication table's DFA enter image description here

I apology for the miss draw, but I hope its readable.

Now I have taken the input "abcb" and applied it on the above NFA, and I have gone through this tree 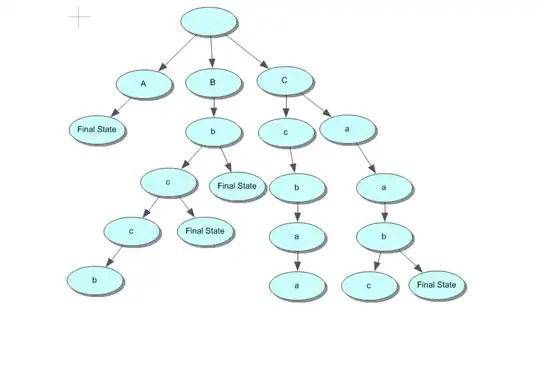enter image description here

As you can see here that the input is all consumed at the branch "C" and I could reach the Final State. Would someone elaborate to me how can I backtrack from that branch which is "C" in this case and indicate that the "C" is the state which shall be marked as the Final State my NFA?

Community
  • 1
CSGuy
  • 31
  • 1

1 Answers1

1

Hint: Let the input be $x_1,\ldots,x_n$. As you mention, it is easy to compute the left-associative product $L_n$ "as you go": $L_{m+1} = L_m x_{m+1}$. The right-associative product recurrence has the wrong direction: $R_m = x_{m+1} R_{m+1}$. To cope with that, at each step you have to guess the value of $R_{m+1}$; it needs to be a value which conforms to your earlier guess of $R_m$ and to the value of $x_{m+1}$. At the end, compare your initial guess of $R_1$ to the value of $L_n$. Arrange things so that you only need to keep track of finitely many values of products.

Yuval Filmus
  • 280,205
  • 27
  • 317
  • 514