Let Alice and Bob be two users chosen uniformly at random from a social network (e.g. Facebook). What is the probability that they are friends assuming that they share $k$ mutual friends?
I am interested both in the experimental values (or estimates) from currently existing social networks (e.g. Facebook) and values predicted by random graph models for these social networks.
Okay, this is my approach to this problem. I think the key concept here is the clustering coefficient $c$. The value of $c$ is denotes how likely it is that two nodes are connected by an edge, if the have a common neighbor. In SN-friendship graphs the clustering coefficient is usually high compared to classical random graph models, such as Erdös-Rényi.
What is known about the clustering coefficient of the facebook-graph? If you follow the presentation of this paper, for a node of degree 100, we have $c=0.14$. Assuming that you have 100 friends is a reasonable assumption than it is close to the median degree (about 99, see here) and the average degree (might be around 95, see here).
Lets make the bold assumption, that the events that a tie between two nodes $A$ and $B$ is present if they have friend $X$ in common, are independent. Then we get
$$\begin{align} P[\text{$A$ and $B$ are friends}] & = 1 - P[\text{$A$ and $B$ are not friends}] \\ &=1-(1-c)^k. \end{align}$$
A plot of this function looks like this:
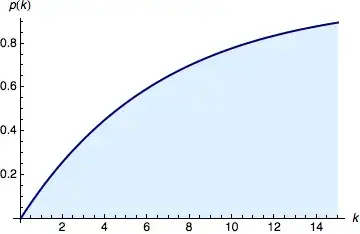
So if $A$ and $B$ have 5 friends in common it is slightly more likely they are friends, than they are not.
This is just a rough calculations that ignores several effects.
