Update 3 and corrected answer
There's an error in the linked solution set (see update 2 below), but it can be easily corrected with @Yuval Filmus's suggestion in the question's comment, which further allows us to rule out one of the possibilities mentioned in the solution set.
This proof hinges on two facts: one, that there is exactly one path between any two nodes in a binary tree; and two, $d(x,y)=d(y,x)$.
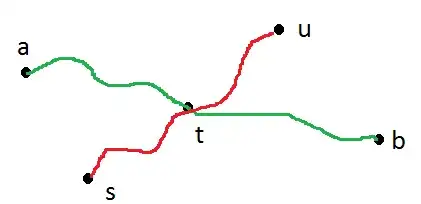
Let $s$ be the root of the first BFS and let $u$ be the final vertex discovered (which means that $u$ must be the farthest point from $s$). Also, let $d(a,b)$ be a diameter. Clearly, $a$, $b$, and $u$ must all be leaves, since otherwise $d(a,b)$ wouldn't be a diameter, and $u$ wouldn't be discovered last (if any of the nodes had children, they would no longer be endpoints of paths of "maximal length", as you could just extend the path by exploring their children). Let $t$ be the lowest common ancestor of $a$ and $b$.
We claim that $t$ must be an ancestor of $u$. Suppose that it were not, then let $r$ be the lowest common ancestor of $u$ and $t$.
$d(u,s)=d(u,r)+d(r,s)$, so we have $d(u,s) \geq d(u,r)$.
Since $u$ was discovered last, $d(u,s) \geq d(a,s)$. Since $d(a,s)=d(a,r)+d(r,s)$, and $d(u,s)=d(u,r)+d(r,s)$, therefore, $d(u,r) \geq d(a,r)$.
Since $r$ is an ancestor of $t$, and $r \neq t$ (since $t$ is not an ancestor of $u$, yet $r$ is), $d(t,r) \geq 1$. Since $d(a,r)=d(a,t)+d(t,r)$, $d(a,r) > d(a,t)$.
Thus, since $d(u,r) > d(a,t)$, $d(u,r) + d(r,t) + d(t,b) > d(a,t) + d(t,b)$
$\to d(u,b) > d(a,b)$, contradicting the fact that $d(a,b)$ is a diameter (since diameters are supposed to be paths of maximal length).
Hence, $t$ is an ancestor of $u$.
Since $u$ was discovered last, $d(s,u) \geq d(s,a)$. Since $d(s,u)=d(s,t)+d(t,u)$, and $d(s,a)=d(s,t)+d(t,a)$, $d(t,u) \geq d(t,a)$. Since $d(t,u) \geq d(t,a)$, $d(b,t)+d(t,u) \geq d(b,t)+d(t,a) \to d(b,u) \geq d(b,a)$.
Since $d(a,b)$ is a diameter, $d(b,a) \geq d(b,u)$.
Therefore, since $d(b,u) \geq d(b,a)$ and $d(b,u) \leq d(b,a)$, $d(u,b) = d(a,b)$.
Therefore, $u$ is the endpoint of some diameter, and thus the second BFS works (the longest path from an endpoint of a diameter must be a diameter).
Update 2
Note that the linked solution set contains an error:
If the paths $p_1$ from $s$ to $u$ and $p_2$ from $a$ to $b$ do not share edges, then the path from $t$ to $u$ includes $s$.
Consider the following counterexample: suppose $s$ is the root of the first BFS tree, and $t$ is the lowest common ancestor of leaves $a$, $u$, and $b$. No edges are shared; only the vertex $t$ is shared. Let $d(a,t) = d(b,t) = d(u,t) = 2$, and let $d(s,t)=1$. Finally, suppose $u$ is discovered last in the BFS. Then $d(a,b)$ is a diameter, $t$ is the first node discovered on that path, and the path from $t$ to $u$ does not include $s$.
To fix this, it's probably necessary to change "do not share edges" to "do not share vertices, as suggested by @Yuval Filmus.
Update
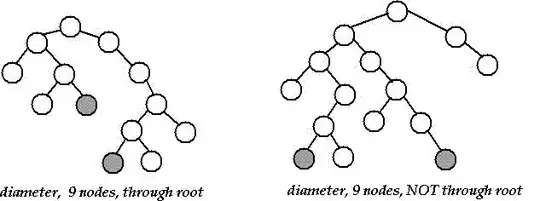
As @j_random_hacker points out in the comments, Lemma 1 below is not sufficient to show that $u$ is an endpoint of some diameter. Hence, the below proof is incomplete.
Original incorrect answer
Suppose we have $d(a, b)$ being a diameter, but we don't know which vertices $a$ and $b$ are, so we start a BFS from some vertex $s$.
If $s = a$, then the first BFS would yield either $b$ or some node $b'$ equally distant from $a$, and the second would either go back to $a$ or to some equally distant node $a'$, and the scheme obviously works. Similarly, if $s = b$, then two BFS would work for the same reason.
Otherwise, we have $s \neq a, b$.
Lemma 0: Both $a$ and $b$ are leaf nodes in the tree rooted at $s$.
Proof 0: If they weren't leaf nodes, we could increase $d(a,b)$ by extending the endpoints to leaf nodes, contradicting $d(a, b)$ being a diameter.
Lemma 1: At least one of $d(s,a)$ and $d(s, b)$ is the largest possible value of $d(s,u)$ for all $u$.
Proof 1: Suppose we have a $u$ that violates the lemma. $u$ cannot be a descendent of $a$ or $b$ since they are leaves from Lemma 0, and $u$ cannot be an ancestor, since that would make it closer to $s$, and it would no longer be able to violate the lemma. Let $t$ be the lowest common ancestor of $a$ and $b$. If $t = s$, then both $d(a, u)$ and $d(b, u)$ would be greater than $d(a, b)$, a contradiction. Otherwise, $t \neq s$ and either $u$ is a descendant of $t$, or not.
If $u$ is a descendant of $t$, then since $d(s,u)$ is greater than both $d(s, a)$ and $d(s, b)$, we have $d(t,u)$ is greater than both $d(t, a)$ and $d(t, b)$ and thus $d(a, u)$ and $d(b,u)$ are both greater than $d(a,b)$, a contradiction since $d(a,b)$ is a diameter.
If $u$ is not a descendant of $t$, then let $w$ be the unique ancestor of $u$ such that $d(s,t) = d(s,w)$. We know $w$ exists because $d(s,t) < d(s,u)$. Then, we have $d(t, b) < d(w,u) < d(t,w) + d(w,u) = d(t,u)$ and thus $d(a, u) = d(a, t) + d(t, u) > d(a, t) + d(t, b) = d(a, b)$, again contradicting $d(a, b)$ being a diameter.
Main result: Starting from any root $s$ and performing a BFS will result in some $a$ being discovered last. Using that $a$ as the root of a second $BFS$ will result in $b$ being discovered last, with $d(a,b)$ guaranteed to be a diameter.
proof: From lemma 1, the first BFS will find an $a$ that is furthest from $s$, which is guaranteed to be one of the endpoints of a diameter. The second BFS will find that diameter, since in a tree there's exactly one simple path between any two nodes.