regular expression for $\{w\in \{a,b\}^*\mid |w|_a \mod 2 = 0\}\setminus \Sigma^*aab\Sigma^*$

Question

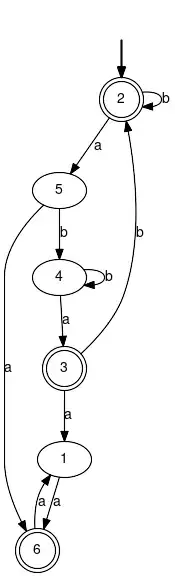
The question asks to write down a regular expression $r$ indicating the language of all the words above $\Sigma = \{a, b\}$ , in which the number of $a$ is even and there is no sub-word $aab$ in them.

I am aware of the fact that there is an algorithm that converts a finite automaton into a regular expression.

I want to know if there is a systematic way of working that does not use this algorithm and will give an appropriate regular expression.

I have written $r = b^*(aa)^* + (b^*ab^+ab)^*(aa)^*$

This is an incorrect answer.

I tried to fix it, but I feel like I'm just adding expressions and can't understand how to work on the problem thoroughly.

Answer 1

The only systematic ways to find regular expression I know of are using automata. As D.W. mentionned in his comment, I am not sure why you are rejecting this method.

A non-systematic approach for this language could be as follow.

The language of words without $aab$ as substring can be represented with the regular expression $(ab\mid b)^*a^*$.

To ensure that a word has an even number of $a$'s, we must consider two cases:

• either the longest suffix of $a$'s is of even length, so there must be an even number of substring $ab$. This corresponds to $(abb^*ab\mid b)^*(aa)^*$
• or the longest suffix of $a$'s is of odd length, so there must be an odd number of substring $ab$. This corresponds to $(abb^*ab\mid b)^*abb^*a(aa)^*$.

Combining the two regular expressions, we get: $$(abb^*ab\mid b)^*(\varepsilon\mid abb^*a)(aa)^*$$

Answer 2

Hint: Here is an automaton for this language