Is $L=\{a^nb^m : n\neq 7m, \ n,m\in \mathbb{N}\}$ context free?

Question

I'm asked to categorize the language $L=${$a^nb^m : n\neq 7m, \ n,m\in \mathbb{N}$}, therefor I need to distinguish if it's regular, context free, or non context free (in $P$)

We know CFLs are closed under union, and I belive $L_1=${$a^nb^m : n<7m$} can be represented by the CFG $S\rightarrow Ab | aAb | aaAb | ... |aaaaaaAb \\\ A\rightarrow Ab | aAb | aaAb | ... |aaaaaaAb | \epsilon $

(I'm not completely sure in the correctness of this CFG, but I belive it shows the idea of $L_1$)

However I am unsure on how to represent $L_2=${$a^nb^m : n>7m$} in CFG form, it seems like the construction rules of $L_2$ would be 8 appearences of $a$ per $b$, but theres no upper limit on the number of appearences of $a$, which got me in a freeze in progressing with this.

this prevents me from claiming that $L_1\cup L_2=L$ is CFL under closure properties

A little edit: I've created this PA: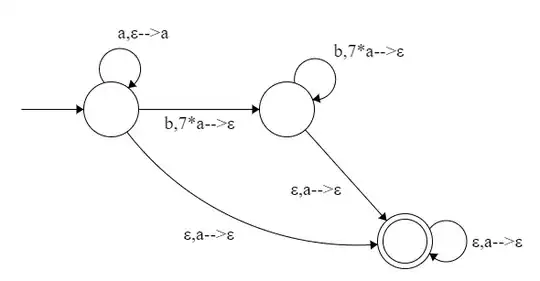

which I believe accepts $L_2$, the basic logic behind it is : read all $a$'s, for each $b$ you see take out 7 appearances of $a$, if you have any $a$'s left in your stack, you can accept the word.

Again, I'm unsure in the correctness of this PA, yet I cant come up with a word in $L_2$ that wont be accepted by this PA.

Answer 1

An easy way prove the language context free is to use the closure properties of context-free languages.

Note that the following grammar with start variable $S$ generates $L' = \{a^nb^m : n = 7m\}$

$$S \to a^7Sb | \varepsilon.$$

Therefore

$$L_1 = a^+L' = \{a^nb^m : n > 7m\}$$

and

$$L_2 = a^+ \setminus L' = \{a^nb^m : n < 7m\}$$ must be context-free, since the context-free languages are closed under concatenation $\circ$ and (left) quotient $\setminus$ with regular languages. Thus $L = L_1 \cup L_2$ must be context-free as well.

---

One way to prove that $L$ is non-regular is to show that the language has an infinite number of unique quotients. We have

$$a^k \setminus L = \{a^{n - k}b^m : n \geq k \text{ and } n \neq 7m\}.$$

But since for all $k_1 \neq k_2$ follows that $b^{k_1} \notin a^{7k_1} \setminus L$ and $b^{k_1} \in a^{7k_2} \setminus L$, it follows that for arbitrary $k_1, k_2$

$$a^{7k_1} \setminus L = a^{7k_2} \setminus L \iff k_1 = k_2.$$

So $L$ must have an infinite number of quotients and can't be regular.

Answer 2

You add either 0 to 6 a's on the left and one or more b's on the right, or you add one or more a's on the left. Then you add 7 a's on the left and one b on the right zero or more times.