Minimum Number of Unique Identifiers for a Grid of Cells

Question

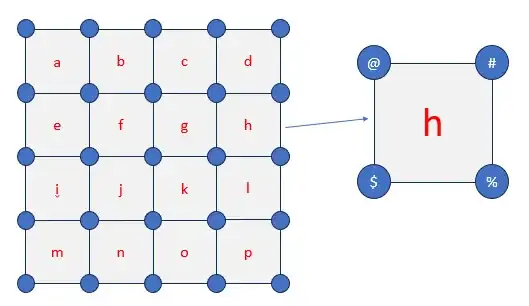
I have a grid of cells, X cells wide by Y cells high. Each cell has four corners, NW, NE, SW and SE. Each corner is shared with adjacent neighbors; i.e., a cell's SW corner is the NW corner of the cell just below it.

In any grid of (X,Y) cells, there are (X+1,Y+1) corners.

In this grid, each corner can be assigned an arbitrary identifier, giving the cell an 'address' of the format NW-NE-SW-SE

In this image below, for cell 'h' the four corners are named @, #, $ and %. The NE corner of cell 'g' would also share the corner name '@'. Cell 'h' would have the address @#$%

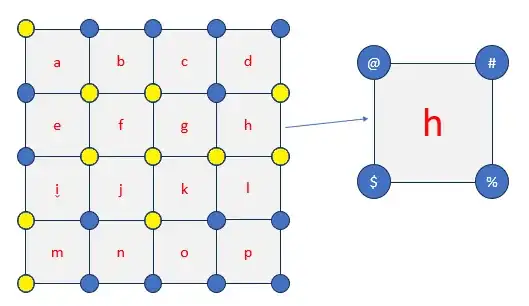
What is the minimum number of unique identifiers needed to allow all cells to have a unique 'address'?

Is there a generalized algorithm or pattern one might use to calculate such a list of identifiers and to assign them to all the corners in a grid of size (XY)?

Thanks in advance!

Edited to add: My purpose in asking this question is to solve a real-world problem, which I did not originally state in my question, and further, that I don't necessarily need the theoretical or provable 'minimum set of unique symbols' but rather an algorithm that combines the properties of a) being easy to understand and implement and, b) provides fairly good answers (i.e., small, perhaps not smallest). Very subjective, I know.

Answer 1

This is one of the 800 possible optimal (2-colour) solutions (including reflections and rotations) to the 4x4 problem, found using an exhaustive search:

The optimality is because 16 cells require 16 distinct 4-digit labels, which exhausts the set of 4-bit patterns. The next "interesting" problem size (in the sense that a "perfect" solution might be possible) is $3^4=81$ cells (so 9x9, 27x3 or 81x1), which would exhaust all 4-digit base-3 numbers -- but this is much too large to check with a dumb brute-force search.

Larger grids can be tiled with a pattern like this, using fresh pairs of colours for each copy. It's then advantageous to use a slightly less "efficient" base pattern that contains no monochromatic cells (the optimal solution above necessarily contains a blue and a yellow monochromatic cell) -- since then you can reuse each colour with every other colour. In other words, $k$ colours permit $k \choose 2$ copies of the base pattern if it is free of monochromatic cells, rather than just $k/2$ copies.

Tiling-based solutions will in general not be optimal. I don't yet see any better way to attack the problem of finding optimal or boundedly approximate solutions other than brute force on a case-by-case basis with a SAT or ILP solver, as suggested by D.W.

Answer 2

You can solve the problem using at most $\left\lceil \sqrt{2X} \right\rceil + \left\lceil \sqrt{2Y} \right\rceil + 3$ identifiers as follows:

PART 1:

Let $G$ be a complete graph over $\left\lceil \sqrt{2X} \right\rceil + 1$ vertices if the $\left\lceil \sqrt{2X} \right\rceil + 1$ is odd; otherwise $G$ be a complete graph over $\left\lceil \sqrt{2X} \right\rceil + 2$ vertices. Each vertex corresponds to a distinct identifier. Note that each vertex in $G$ has even degree. Thus, there exists an Eulerian path in $G$ that can be computed in $O(X)$ time. The path length is at least $X$. In other words, there is a sequence of at least $X$ identifiers such that any pair of consecutive identifiers appears exactly once in the sequence. Lets name this sequence $S_X$.

Use the sequence $S_X$ as the first row of the grid. This ensures that all the cells in the first row have distinct addresses.

Now use the same sequence for each odd numbered row in the grid. This ensures that all the cells within the same row have distinct addresses.

$\text{}$

PART 2:

To ensure that the cells in the same column have distinct addresses, take a new set of $\left\lceil \sqrt{2Y}\right\rceil+1$ identifiers. Let this idetifier set be $I_Y = \{y_1,\dotsc,y_t\}$ for $t = \left\lceil \sqrt{2Y} \right\rceil + 1$. Construct $I_Y \times I_Y$. Let $p = \{y_i,y_j\}$ be any pair of identifiers in $I_Y \times I_Y$. Let $(y_i,y_j,y_i,y_j,\dotsc,y_i)$ be an alternating sequence of these two identifiers. Use this sequence for any even numbered row of the grid. Since there are at least $Y$ such distinct pairs, each grid vertex is now labeled. Note that all the cells in the same column have distinct addresses since they have different $\{y_i,y_j\}$ pairs. Thus all the cells in the grid have the distinct address too. This completes the proof.

---

Note that you can solve the problem using at most $\left\lceil \sqrt{X} \right\rceil + \left\lceil \sqrt{Y} \right\rceil$ identifiers as well using directional edges in the part $1$ of the above construction and more careful analysis of part $2$.

Answer 3

For a pragmatic solution, I suggest using a SAT solver.

Suppose we want to find a valid coloring, using $C$ colors. Let $L=\lceil \lg C \rceil$, so that each color can be encoded as a $L$-bit integer. Let $x_{i,j,k}$ be a boolean variable, representing the $k$th bit of the color of the corner at position $(i,j)$. for each $i,j$, add the constraint that $x_{i,j,L-1} \cdots x_{i,j,1} x_{i,j,0} < C$ as unsigned integers (this can be expressed as CNF clauses). This will force every corner to be colored with one of the $C$ colors.

Also, for each pair of cells, we encode the requirement that those two cells have different 'addresses', as follows: let $y$ denote the sequence of boolean variables that represents the address of the first cell, and $z$ the same for the second cell. We introduce temporary variables $t_0,\dots,t_{4L-1}$, constrain them so that $t_i=y_i \oplus z_i$ ($\oplus$ represents the logical-xor; this can be enforced with a few CNF clauses), and then add the CNF clause $t_0 \lor t_1 \lor \cdots \lor t_{4L-1}$. This will force $y,z$ to differ in at least one bit position, so that the two cells receive different addresses.

Now feed this entire CNF formula to a SAT solver and see if it finds a solution. You can use binary search over $C$ to minimize the number of colors.

A front-end like Z3 will make implementing this easier.

If I had to guess, I would guess that $\sim (XY)^{1/4}$ colors might suffice, but I have no proof.

Answer 4

Each Even column of corners (blue arrows) encodes a single unique ‘X’ indicator: x0,x2,x4… (here colored using Red, Green, Blue)

Each Odd column of corners (yellow arrows) encode a semi-incrementing ‘y’ indicator y0,y0,y1,y1,y2,y2 (here colored using Cyan, Magenta, Yellow)

Resulting set of required unique symbols is (x+1)/2 + (y+1)/2

While I doubt this is an optimal solution for smallest set of unique symbols, it does have the advantage (for my purposes) of being a simple algorithm to implement.

This method seems very similar to the approach suggested by j_random_hacker in a comment above, but I'm not good enough at all this to understand how similar or divergent they actually are.