There is a chess tournament planned. It is a single-elimination tournament, and for spectacle purposes, only one match at a time will take place, on a table in the middle of the stage. The winner of a match will have to stand offstage if they don't play the next match. The loser will be out of any further consideration immediately.
Luckily, the organisers succeeded in inviting a grand chess champion to the tournament. Let's call him MC (for main character, of course).
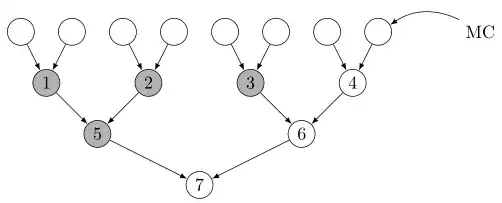
However, MC doesn't like to stand once he's seated. Also, as the grand champion, he's sure to win every match he would play. His condition to come to the tournament is to never stand once he's asked to play. It is quite easy to find a solution: just let all other matches take place and let him come at the end to play the remaining matches. The following figure shows how to do it, where sources are players, internal vertices are matches, blackened vertices are finished matches before MC comes. The matches could take place in order 1-2-3-5-4-6-7 to get what MC wants.
Now consider the following problem: if we don't consider MC as a special player, but just want to minimize the number of times a player has to stand, how to do it. A natural order to play the matches in the previous tree would be 1-2-3-4-5-6-7, but that would result in a total of 5 players standing after a match: winners of match 1,2,3,4,5. The order 1-2-5-3-4-6-7, which is how the organisers would satisfy MC, would result in only 3 players standing after a match: winners of match 1, 5, 3.
This could be generalized to $n=2^k$ players: let $S(n)$ be the number of times a winner has to stand before playing again. Then with the same idea that satisfies MC, we could get $S(2) = 0$ and $S(n) = 2S(n/2) + 1$, meaning $S(n) = \frac{n}2-1$, which is better than the $n-3$ naïve order .
Is this the optimal strategy? This looks like it, but who knows.