AVL trees are height balanced binary search trees. As a consequence of this balance, the height of an AVL tree is logaritmic in its number of nodes. Then, searching and updating AVL-trees can be efficiently done.
The fact that AVL-trees have logaritmic height can be shown by analyzing "minimal" AVL-trees, where for each internal node the height difference between subtrees is $\pm 1$. Those trees have a Fibonacci number of nodes (minus one) and hence the number of nodes in a tree of height $n$ is approximately $\varphi^n/\sqrt 5$, where $\varphi$ is the golden ratio. See: AVL tree worst case height proof
A less precise analysis shows that half of the levels of an AVL trees must be completely filled. This can be shown by induction. This leads to an lower bound on the number of nodes in the form of $2^{n/2}$ which is sufficient for proving logaritmic height. See AVL tree height log n proof
Now here is my question: Is is easy to argue that half of the levels of an AVL tree are completely filled? I am looking for a good argument that directly uses the definition of AVL trees, without the induction on the two subtrees.
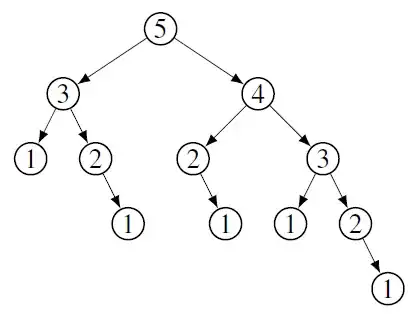
Picture below has a Fibonacci tree with height 5 (counting the nodes) and three levels are completely filled.