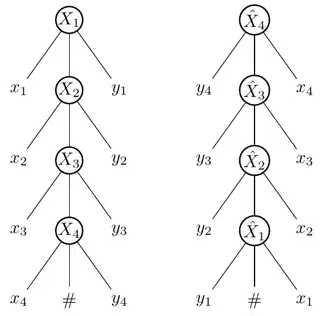
Given that $\#\notin \Sigma$ and $L\subseteq \Sigma^*\#\Sigma^*$, prove that if $L$ is context-free language then $L' = \{w_2\#w_1 \mid w_1\#w_2\in L\}$ is context-free. I'm trying to prove this in this way:
- because $L$ is context-free then $G$ is context-free grammar for $L$, then $L(G)=L$.
- by showing that the reversed grammar $F$ of $G$ is the same grammar of $L$ and because $G$ is context-free then $F$ is context-free then $L(F)=L'$ is also context-free. but can't figure out a way to prove this, so I need help to do this.