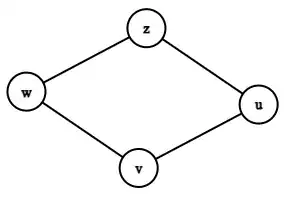
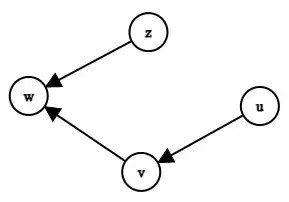
Studying for my finals and stuck on the following question:
Prove or disprove: Given an undirected and connected graph $G=(V,E)$ and three different vertices $u,v,w\in V$ then there exists some number $x$ so in any run of BFS from vertex $w$, the distance from $u$ to $v$ in BFS tree is always $x$.
I think it's not true but could not think about a good example to disprove it.