Greetings all and thank you. I'm a Ph.D. candidate working on a force structure's 3D tessellation project and get stuck.
I've simplified the system into a set of lines linked together which formed a Line-Framework (points connectivity list). Now I want to get the tessellation of this Line-Framework in a set of minimal convex polyhedra without changing the connectivity of the points. Let me give an example for further description.
The Line-Framework is described in points pairs, e.g.{{P1,P2};{P2,P3};{P2,P9}...}, which can be drawn as follows. Each point Pi has coordinate details.(And all the lines are the same length.)
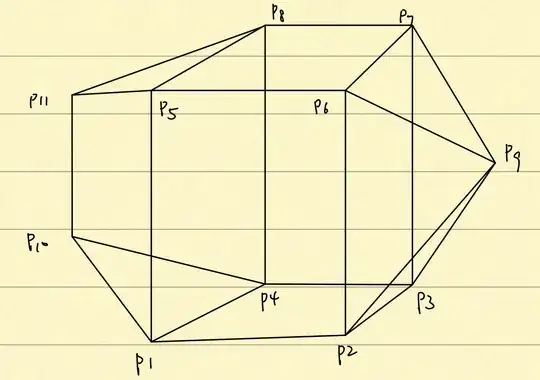
And I want to have the convex set {v1={P1,P2,P3,P4,P5,P6,P7,P8};v2={P9,P2,P3,P6,P7};v3={P10,P11,P1,P4,P5,P8}}; V=v1+v2+v3. How can I workout the points set collections I need?
I've tried Delaunay triangulation but merging tetrahedra is complicated. THANKS!
The Line-Framework describes the system of a pack of spheres. Each $P_i$ is the center of the sphere, and $\{P_i,P_j\}$ means that the sphere $S_i$ contacts with $S_j$. The length of $\{P_i,P_j\}$ is $|P_i,P_j|=R_i+R_j$.