I'm implementing a stable integer sorting algorithm, I've chosen radix sort. I've tested LSD vs MSD implementation, wrote MSD/LSD hybrid implementation to reduce bandwidth pressure. The repo is here: https://github.com/KirillLykov/int-sort-bmk
Now some Figures to discuss.
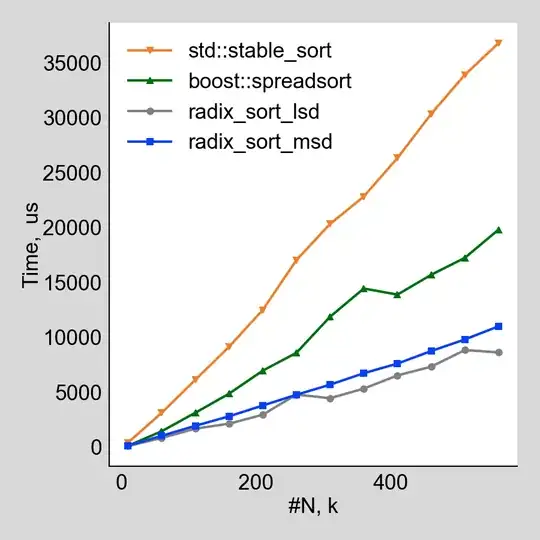
First of all, radix sorts outperform significantly stable_sort on shuffled unique values in the range 0..N, where N is number of elements in the array:
On an input of randomly generated (uniform) numbers in the range 0..1e9, LSD outperforms other sorting algorithms, but MSD doesn't:
I don't have a good explanation for the last observation.
But it hinted to develop a combined radix sort implementation which will rely on MSD first and when the size of the range is smaller than 2^14 use LSD.
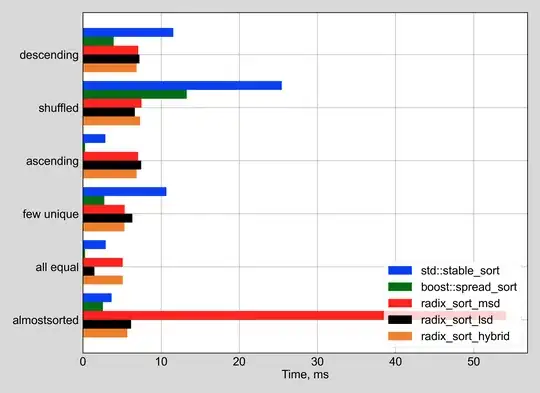
I've benchmarked these implementations on different distributions:
Observation is that although radix sort outperforms on random data, it performs poorly on some specific cases.
I think that a good approach is to define a criterium when/when-not use radix sort depending on the input data.
This approach was implemented in boost::spreadsort -- knowing the size of the input, min/max values they make a decision whether to use bucket sort one more time or to rely on another sorting algorithm. See for example boost::spread_sort implementation
Probably, it is possible to adapt the same analysis for radix sort yet not sure because I couldn't reverse engineer the the math behind these checks (I've read the report).
So the question is you have any ideas on how to develop criterium for using other sorting algorithms based on some (cheap to compute) observations about the input data?