Is the following problem NP-hard? (or have you seen it before?)

Question

I genuinely don't know if the following problem is NP-hard. I have never seen it mentioned online, but it's hard to even search for exact problems like this. I have been trying to find an efficient algorithm for a while and intuitively it feels very NP-complete to me, but I haven't been able to prove it. A solution would be directly applicable to my work, if it could be found.

---

Problem: Assume you have $N$ different tasks which each have a unique integer length $l_n$. These tasks are arranged in a dependency tree so that each task can only be started after zero or more other tasks are completed. You also have $M$ different resources. Each task requires a given resource and each resource can only be used by one task at a time. What ordering of tasks allows for the fastest completion of the overall program (based on maximizing the amount of tasks that can be parallelized).

Example: In less abstract terms, imagine that each task is a step in a recipe. The resources are elements of a kitchen like an oven or mixer. If cooking one part of a meal requires a short use of the oven followed by a lot of manual work, and cooking the other part of the meal requires a long oven time, you should schedule the shorter cook first so that you can do the rest of the work for that component while the other half is in the oven.

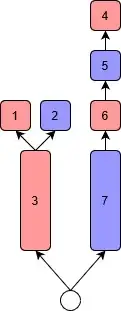
Another example: Consider the dependency tree below. $a \rightarrow b$ indicates "$a$ depends on $b$". The length of a block indicates the time it takes to complete (1 or 3 in this case). There are two resources/channels: red and blue.

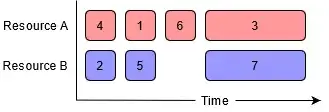
An example solution might look like this:

This shows that a greedy approach (like scheduling (1) and (2) simultaneously) is not sufficient -- you have to look ahead to minimize waiting for resources.

Answer 1

This problem (more formally its decision version) is NP-complete.

NP-hardness can be shown via a reduction from the Job-Shop Scheduling Problem (JSP) with makespan objective, which is well-known to be NP hard.

In the JSP, we have $n$ jobs $J_1, J_2, ..., J_n$. Within each job there is a set of operations $O_1, O_2, ..., O_n$ which need to be processed in a specific order. Each operation $o$ has a specific machine $m_o \in M$ that it needs to be processed on and only one operation in a job can be processed at a given time. (adapted from Wikipedia)

Now it is easy to see that JSP is just a special case of your proposed problem (one task per operation of JSP, dependencies only between successive operations in a job), which makes it at least NP-hard too.

Membership in NP can be shown by guessing an optimal schedule and verifying in polynomial time that it fulfills all constraints.

Answer 2

What you are describing is a planning and scheduling problem. Kautz and Selman pioneered the use of Boolean satisfiability and SAT solvers to attack such problems in the early 1990's. SATPLAN, STRIPS, and PDDL are good search terms for further research. There seem to be several planner implementations that take world descriptions written in STRIPS and generate a plan that minimizes plan length, ordering tasks to take advantage of time savings produced by tasks that can be executed in parallel. Given how effective SAT solvers are at attacking planning instances, I'd guess that the average-case hardness of planning problems is low, but I wouldn't be surprised if the general problem turned out to be NP-hard.

Answer 3

Thanks to "user2357112 supports Monica" for pointing out issues! Now fixed.

Let's formulate the decision problem form of this problem, which I'll call Tree Scheduling (TS):

Given a number $k$, and a rooted tree with

• tasks $t_1, \dots, t_n$ for vertices, each having some integer duration $l_i$ and requiring some resource $r_i$ from a set $S$ of resources, and
• arcs representing dependencies between tasks,

is there a schedule that satisfies all dependencies, avoids scheduling two jobs that use the same resource at overlapping times, and completes within $k$ time units?

This problem is NP-complete even with just two resources, by reduction from Partition (PART).

In PART, we are given a multiset of $m$ numbers $a_1, \dots, a_m$ having $\sum_i a_i = T$, and the task is to determine whether we can partition them into two multisets, each having sum $T/2$. Given an instance of PART, we construct an instance of TS with:

1. A root task $t_r$ using resource 1, of duration 1;
2. For each $1 \le i \le m$, a task $t_i$ using resource 1, having duration $l_i = a_i$ and on which $t_r$ depends;
3. A task $t_{after}$ using resource 2, of duration $T/2$ and on which $t_r$ depends;
4. A task $t_{sep}$ using resource 1, of duration 1 and on which $t_{after}$ depends;
5. A task $t_{before}$ using resource 2, of duration $T/2$ and on which $t_{sep}$ depends;
6. $k=T+2$.

The idea is that an optimal solution to an instance consisting of just $t_r$, $t_{before}$, $t_{sep}$ and $t_{after}$ takes time $T+2$, since these tasks are on a critical path of this length. This solution has 2 "gaps" of length $T/2$ in the usage of resource 1. After adding the tasks $t_1, \dots, t_m$, we can still complete all tasks in $T+2$ time iff we are able to fill up each gap with exactly $T/2$ time units' worth of tasks.

Answer 4

It is NP-Hard as others have said, but... sometimes there is an easier way to solve it. You can do a Lagrangian relaxation to essentially remove the NP-hardness solve that problem, and then use that as an initial guess for the original problem. Pekny and Miller essentially did something like to for the Asymmetric Traveling Salesman problem. They reduced it to an assignment problem (n^3), and the used that to stich together a solution to the original problem. where they could stich together the cycles without adding cost, they had a guaranteed optimum in polynomial time - FOR FORTUITOUS DATA SETS. But having a fortuitous data set might end up being most of the time.