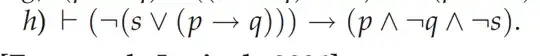2

I'm stuck on how to progress with this proof, despite I have tried, I cannot see the next move.

Given this proof without predicate:

Proof

So far what I've accomplished:

My approach

My idea is, as I can't see any other option using (-(Sv(P->Q)) as the first assumption in order to introduce a conditional, so the assumption must end in P ^ -Q ^ -S. As you can see I have obatined -Q and -S but, how do I proof P?

SOLUTION:

sol

Juho
  • 22,905
  • 7
  • 63
  • 117
Jesús Díaz Castro
  • 23
  • 4

1 Answers1

3

It is a bit hard to say exactly which introductions you should perform since we don't have your rule set, but I think the over all strategy should be as follows:

From $\neg (S \lor (P \to Q))$ you get $\neg (P \to Q)$. Since you have $\neg Q$, you should try to introduce $\neg P$ and thus obtain $P \to Q$. That should be a contradiction and you can conclude $P$.

Ainsley H.
  • 17,823
  • 3
  • 43
  • 68