Matching superimposed image

Question

We are given two grayscale images, one of which contains a large, mostly contiguous patch from the other one. The patch can be altered with noise, its levels may be stretched, etc.

Here's an example

We would like to determine the region of the image which was copied onto the other image.

My first instinct was to look at the local correlation. I first apply a little bit of blur to eliminate some of the noise. Then, around each point, I can subtract a gaussian average, then look at the covariance weighted by that same Gaussian kernel. I normalize by the variances, measured in the same way, to get a correlation. If $G$ is the Gaussian blur operator, this is:

$$ \frac{G(A \times B) - G(A)G(B)}{\sqrt{(G(A^2)-G(A)^2)(G(B^2)-G(B)^2)}}$$

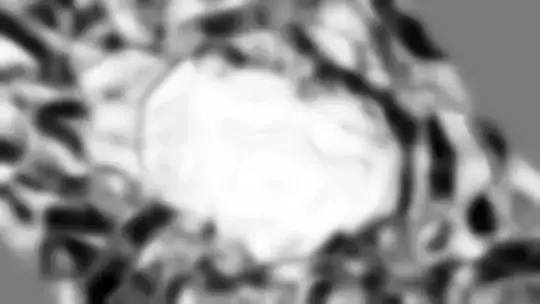
The result is... not too bad, not great:

Playing with the width of the kernel can help a bit. I've also try correlating Laplacians instead of the images themselves, but it seems to hurt more than it helps. I've also tried using the watershed algorithm on the correlation, and it just didn't give very good results.

I'm thinking part of my problem is not having a strong enough prior for what the patch should be like, perhaps a MRF would help here? Besides MRF, are there some other techniques, perhaps more lightweight that would apply? The other part is that correlation doesn't seem to be all that great at measuring the distance. There are places where the correlation is very high despite the images being very visually distinct. What other metrics could be of use?

Answer 1

Normalized correlation works very well to compensate contrast stretching. In fact, it works too well for your taste. When you match two pretty uniform, featureless areas, the correlation will be good even if their average levels mismatch completely. Simply because uniform areas are alike.

You can't have your cake and eat it too. If you want to drop the contrast invariance, use an unnormalized correlation. Otherwise, you can disregard regions of high correlation where the variance is low, or revert to comparison of the means.

Answer 2

I will assume the patch is the same position and is unchanged. Given this, you could try a two-step procedure with basic image processing methods:

Step 0 (optional): Align/register the two images.

Step 1: Compute local image similarity, on a pixel-wise basis.

Step 2: Find a large connected region in that similarity map where there is high similarity.

---

For Step 1, one approach is local correlation, as you used. You could also try normalized cross correlation if you think one image might be shifted slightly (e.g., by a subpixel amount). Another is to compute the square of the pixelwise difference of the two images. Yet another possibility: at coordinate $(x,y)$, extract a patch 7x7 patch from each image centered at $(x,y)$, compute some measure of image similarity (e.g., L2 distance, local correlation, you name it; possibly preceded by some image registration step) between those two patches, and use that as the similarity measure at $(x,y)$; do this for every coordinate.

For Step 2, you are looking for a large connected region with a high similarity score. One approach is to threshold followed by connected components. Another approach is a watershed transform. Another approach is to use image morphological operators (e.g., opening) followed by one of these methods. More generally, you could look at methods for blob detection.

With image processing tasks like this, you may need to experiment with a bunch of different methods and see which ones work well. When you experiment, I recommend that you implement, measure its effectiveness, also look at a random sample of 5-10 images and the results of the analysis on those images, and look at a random sample of 5-10 images that got handled incorrectly. This visualization can be helpful in understanding in what situations a method fails, which can sometimes suggest improvements to address those particular situations.