What is the running time of generating all $k$ combinations of $n$ items $\binom{n}{k}$?

Question

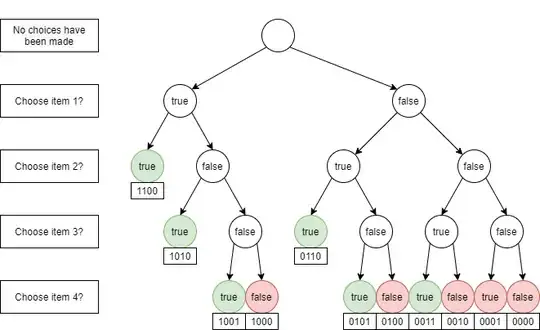
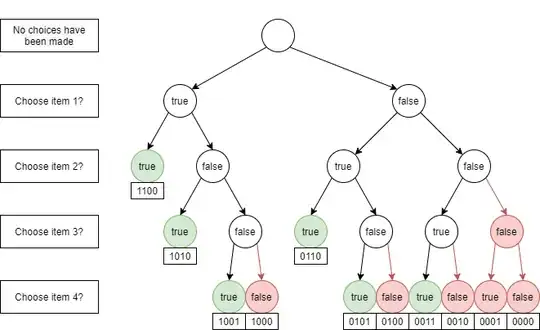
I was solving the following problem, just for reference (441 - Lotto). It basically requires the generation all $k$-combinations of $n$ items

void backtrack(std::vector<int>& a,
               int index,
               std::vector<bool>& sel,
               int selections) {
    if (selections == 6) { // k is always 6 for 441 - lotto
        //print combination
        return;
    }
    if (index >= a.size()) { return; } // no more elements to choose from
    // two choices
    // (1) select a[index]
    sel[index] = true;
    backtrack(a, index+1, sel, selections+1);

    // (2) don't select a[index]
    sel[index] = false;
    backtrack(a, index+1, sel, selections);

}

I wanted to analyze my own code. I know at the top level (level = 0), I'm making one call. At the next level (level=1) of recursion, I have two calls to backtrack. At the following level, I have $2^2$ calls. The last level would have $2^n$ subproblems. For each call, we make $O(1)$ work of selecting or not selecting the element. So the total time would be $1+2+2^2+2^3+...+2^n = 2^{n+1} - 1 = O(2^{n})$

I was thinking since we're generating $\binom{n}{k}$ combinations that there might be a better algorithm with a better running time since $\binom{n}{k}=O(n^2)$ or maybe my algorithm is wasteful and there is a better way? or my analysis in fact is not correct? Which one is it?

Answer 1

Obviously your code will be lower bounded by $\Omega \left(n \choose k \right)$ since you can't skip any combinations, then you wouldn't be generating them all.

With this in mind we can do a little better analysis on the bound. Let's take a look at the recursion tree for this. Let's use a small example like 4 choose 2. Here is how your algorithm would work:

This generates all valid choices of 2 elements from 4 (seen in green). At this point you may realize that your algorithm actually generates some invalid combinations for 4 choose 2 (seen in red).

If we had a completely full tree that never terminated early (at selections == k) then it would be easy enough to show that this runs in $O(2^n)$ if you just sum up the levels. However our tree ends early for a lot of branches and when $k$ is small and $n$ is large this would be much less than $O(2^n)$.

Let's say your code doesn't consider invalid possibilities. This should make analysis easier so that there are only $n \choose k$ leaf nodes. We would prune these branches (in red):

This would be easy enough to do with a if ((a.size() - index) <= (k - selections)) return; check.

Now if this is the case then we know there are only $n \choose k$ leaf nodes in our recursion tree. We also know that the longest path from root to leaf would be $n$ so we can easily upper bound this by $O(n \binom{n}{k})$ which is better than the $O(2^n)$ we previously discussed.

If you assume printing the combination takes $O(n)$ then this is the best we can do since the printing time complexity would dominate the leaf depth complexity.

---

You could attempt to do a little better if you assume that printing takes $O(k)$ which you may be able to manage.

We can get a little better accuracy with this. For example, we know there's exactly 1 leaf node at depth $k$ (i.e. pick the first $k$ elements). We also know there will be exactly $k$ leaf nodes at depth $k+1$ since this is essentially the scenario where we do choose the $k+1$st element and we don't choose 1 of the first $k$ nodes (i.e. $k \choose 1$ or equally $k \choose k-1$). Similarly the # of leaf nodes at depth $k+2$ would be $k+1 \choose k-1$. Then we can extrapolate this for all leaf depths. At depth $k <= i <= n$ we would have exactly $f(i)$ nodes where:

$$f(i) = \binom{i - 1}{k-1}$$

From this we can determine the time complexity of leaf nodes at depth $i$ as $t(i)$:

$$t(i) = i \cdot f(i)$$

We then sum these up from depth $i = k \ldots n$ for the overall time complexity:

$$\begin{align} T(n) & = \sum_{i = k}^{n} i \binom{i-1}{i-k} \\ \end{align}$$

It ended up getting pretty messy so I'm not going to work it out completely, but in short this will still be $O(n \binom{n}{k})$ and $\Omega(k \binom{n}{k})$.

Answer 2

If you want to generate all items, the runtime is obviously at least O(n over k). To avoid exceeding O(n over k) your algorithm must be quite carefully designed.