Assignment Problem -- finding the $k$ agents with the best assignment

Question

I have a question that I have been thinking about. Suppose we have $n$ agents, $m$ tasks, a cost matrix with $M_{ij}$ being the cost of agent $i$ performing task $j$, and are given a value $k \leq n$. How can we find the $k$ unique agents, who when each optimally allocated a unique task, result in a minimum total cost? Can this be related to the assignment problem? Thank you very much for any guidance or assistance.

Answer 1

The assignment problem can be extended to solve this problem. The regular problem without the $k$ restriction can be solved by building a Minimum Cost Maximum Flow network is as follow:

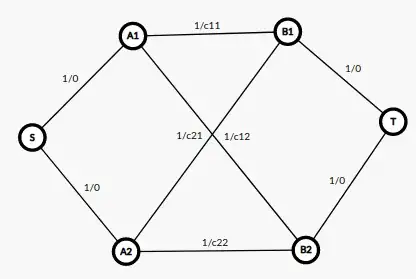
We have a source $S$ a sink $T$ and the corresponding bipartite graph in the middle. Note that each edge has two values $f/c$ which denote maximum flow allowed through this edge and cost of each flow unit. Now, the problem is that we want to allow at most $k$ units of flow from $S$ to $T$. To do this, just duplicate node $S$ into $S_1$ and $S_2$ and put an edge among them such that cost of each unit is 0 (no penalty) and maximum flow allowed is $k$. The new graph will look like this:

The minimum cost maximum flow from $S_1$ to $T$ is the solution to the original problem for a fixed $k$.