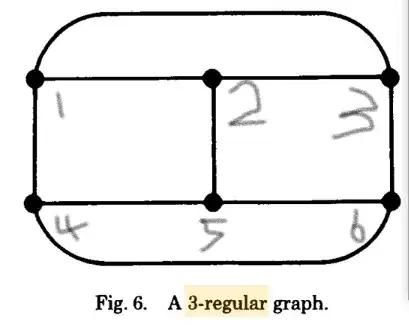
Going through Lamport's paper, I'm a little confused by the second part of the regular set of neighbors definition.
- A set of nodes $\{i_1, \ldots, i_p\}$ is said to be a regular set of neighbors of a node if :
- each $i_j$ is a neighbor of $i$, and
- for any general $k$ different from $i$, there exist paths $y_j,_k$ from $i_j$ to $k$ not passing through $i$ such that any two different paths $y_i,_k$ have no node in common other than $k$.
- The graph $G$ is said to be $p$-regular if every node has a regular set of neighbors consisting of $p$ distinct nodes.
I'm assuming $i_j$ is a node in the set. Is it right to assume $k$ is any other node not $i$ or any node not $i$ and not in the set? Also, is it saying that every $y_j,_k$ path will not have a common node or that there must be some $y_j,_k$ paths that don't share a common node?
I put the example graph from Lamport's paper with some labels on the nodes (that was edited with a track pad. Sorry!) just in case it'll help give an explaination. Any and all help is much appreciated!