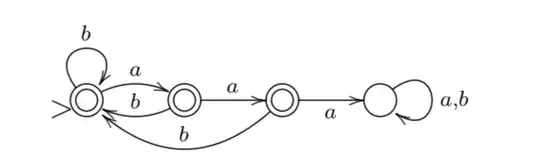
I am trying to find the regular expression that defines this DFA, I am finding this particular case difficult since it has multiple accepting states.
If I understand this DFA correctly, it recognises:
empty strings or strings with any number of b => b*
or
a followed by any number of b => ab*
or
aa followed by any number of b => aa(b*)
So the closest I have got is b*+(a+aa)+(a+aa)b* but I know this is not correct, since it doesn't recognise strings such aabaabab.
I have been using http://ivanzuzak.info/noam/webapps/fsm_simulator/ so I can see I don't know how to make the transition back to Q0 from Q1 or Q2 when there is a b.
I took a look to How to convert finite automata to regular expressions? but the explanations are way above my current level of understanding.
Could anybody help me finding where I'm going wrong and how could I fix it?
Many thanks in advance.