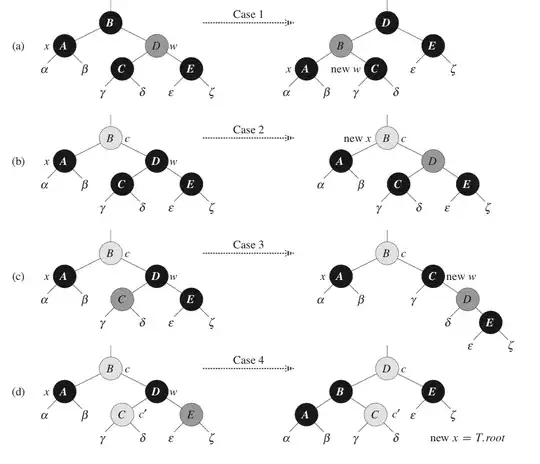
I don't know why case 4 will resolve the issue of the double black of $x$ described in Introduction to algorithm p.329. I know case 1 is transformed into one of {2,3,4} case, and case 2 re-point $x$ to its parent node so it's approaching the root, and case 3 will be transformed into case 4, but both case {3,4} will not change the pointer $x$, anyway so how case 4 work?
Is it because for paths include $C,E$ there is no difference about the number of blacks while for that about $\alpha,\beta$ an extra black node $B$ is passed?