The different bounds of PRP/PRF switching lemma

Question

The PRP/PRF switching lemma is usually denoted as follows:

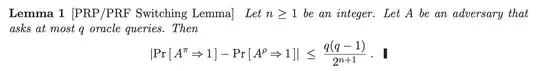
I understand the proof of this version of the bound $\frac{q(q-1)}{2^{n+1}}$ and the game-playing technique behind it.

However, I came across a different version of this lemma recently, which is used more often in papers. It is denoted as follows:

This version of the bound turns out to be $\frac{q^{2}}{2^{n+1}}$ (or something like this). The corresponding proof (Page 150) does not explain why the number of collision pairs is $\frac{q^{2}}{2}$ instead of $\frac{q(q-1)}{2}$ when there are $q$ queries.

So my question is:

Why the bound is $\frac{q^{2}}{2^{n+1}}$ instead of $\frac{q(q-1)}{2^{n+1}}$ in the latter version of this switching lemma ? How to prove it ? Thanks!

Answer 1

The simple answer is, both lemmas are correct and the first one trivially implies the second one. This follows simply because for any $q\in\mathbb{N}$, $q(q-1) = q^2-q \leq q^2$.

Why then do both versions exist? The first one gives a tighter upper bound, if you care a lot about the tightness of the concrete bounds in whatever proof you are using it, then use that one. If the concrete tightness doesn't matter as much you can just as well use the looser because it is quicker to write and easier to read.

The corresponding proof (Page 150) does not explain why the number of collision pairs is $\frac{q^2}{2}$ instead of $\frac{q(q-1)}{2}$ when there are $q$ queries.

It doesn't state that there are $q^2/2$ such pairs at all. What it says is that

there are less than $Q^2/2$ such pairs

which is true, given that there are $Q(Q-1)/2 \leq Q^2/2$ many pairs.

How to prove it?

Well, the proof is in the book, but if you find the proof of Bellare and Rogaway easier to follow, then you can simply use that proof given that it proves a strictly stronger upper bound.