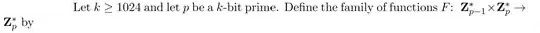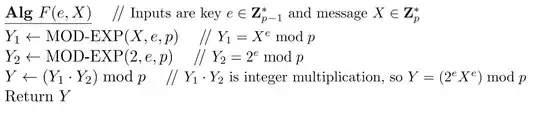Here is the game:
How can I make an $\mathcal{O}(k^2)$-time adversary making only one query to its Fn oracle and achieving advantage $= 1 - 1/(p-1)$
Here is my idea so far: query $2^{-1}$, which when it goes through the Encryption algorithm, will return 1. So,
Adversary A:
C <- Fn(2^{-1})
if C == 1 return 1
else return 0
When we query 2^{-1}: \begin{align} Y_1 &= (2^{-1})^e &\bmod p \\ Y_2 &= 2^e &\bmod p \\ Y &= (2^{-1}\cdot 2)^e &\bmod p \\ &= 1^e &\bmod p \\ &= 1 \text{ (for all e)} \end{align}
Is this allowed? Is it okay to query $2^{-1}$. I am assuming here that $2^{-1}$ is in $Z_p$ as long as $2$ is relatively prime.
Is this Adversary correct?