In quantum cryptography, why can a qubit can be both 0 and 1 at the same?

Question

The texts below are from some tutorial, and it says (in bold format below) a qubit can be both 0 and 1 at the same time. It sounds very strange to me, can you please explain why?

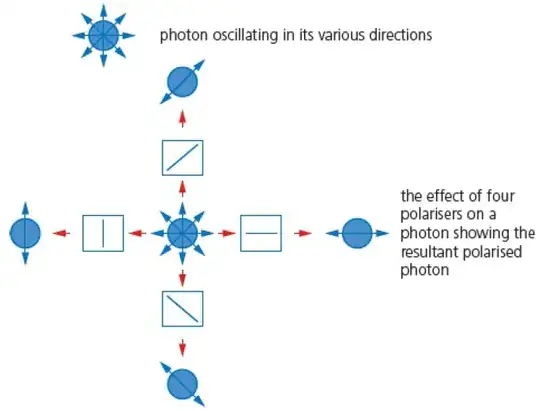
Quantum cryptography utilises the physics of photons (light energy according to the formula E = hf) and their physical quantum properties to produce a virtually unbreakable encryption system. This helps protect the security of data being transmitted over fibre optic cables. Photons oscillate in various directions and produce a sequence of random bits (0s and 1s) across the optical network. Sending encryption keys across a network uses quantum cryptography – a quantum key distribution (QKD) protocol (one of the most common is BB84). QKD uses quantum mechanics to facilitate the secure transmission of encryption keys. Quantum mechanics use a qubit (quantum bit) as the basic unit of quantum data. Unlike normal binary (which uses discrete 0s and 1s), the state of a qubit can be 0 or 1, but it can also be both 0 and 1 simultaneously. Figure 17.5 shows a representation of a photon and how a photon can be affected by one of four types of polarising filter.

Plus, if some of you ever learned A-level computer science, can you please give some recommendation for A-level computer science books, and exercises?

Answer 1

“Both 0 and 1 simultaneously” is a lie-to-children: it's a simplification intended to be comprehensible and not fully accurate. It's not a very good one. A better way to present it is that a qubit is partly 0 and partly 1. It's not a single number, it's a function that takes values between 0 and 1.

As for why… it's physics. Classical physics says that a particle is in a specific location at a specific time. That works very well when you want to calculate the trajectory of a planet in a solar system. It doesn't work when you want to calculate the trajectory of a subatomic particle. It turns out that a better model of physics is that a particle has a presence density: it's all over the universe, but almost all of it is concentrated in a tiny zone. Similarly, a photon's polarization is not just a direction, but a density (which is more or less the same as a probability distribution): there's a certain proportion of it in every direction. And this is still a lie-to-children — more accurately, the density is a complex number.

Obtaining results from a quantum computer involves summing the density functions of many qubits. It's kind of like adding $n$ numbers between $0$ and $1$ and getting a conclusive result if the sum is either close to $0$ or close to $n$, except with more complex math.

Recommended reading: “The talk” by Scott Aaronson and Zach Weinersmith