How to get an output of SHA-1 with first 2-bit are zeros?

Question

Can someone explain what are the ways to get an output of SHA-1 with first 2-bits which are zeros?

Answer 1

Hash random values until you get a hash with two leading zeroes. We would expect about 1 in 4 values to have a hash-value of that form.

So let's try this:

echo hello | sha1sum
f572d396fae9206628714fb2ce00f72e94f2258f  -

Nope.

echo hello1 | sha1sum
0ef562ff2d0c21358f9d289f1c908436714fc923  -

There we are, 4 leading zeroes.

Answer 2

This is an extension of Maeher's answer and the full code of this answer is in Github.

Hash functions are expected to produce random output random in the sense that the value of the hash is basically unpredictable without actual computing. We, also, expect them to produce the hash result evenly, i.e. all possible hash values occur with the same probability. This means that we expect 1/2 of them to have a leading zero, 1/4 them has 2 leading zeroes, and so on. In a formal way; for $n$ trial we expect $n/2^i$ values have $i$-leading zero.

The below Python code experiment this (the below is optimized of the original. It is optimized on codereview at least 2x speed up )

import hashlib
import random
leading = [0] * 160
for i in range(100000):
hashvalue = hashlib.sha1(random.getrandbits(128).to_bytes(16, 'big')).digest()
zeroes = 160 - int.from_bytes(hashvalue, 'big').bit_length()
leading[zeroes] = leading[zeroes] +1


for item in leading: 
    print(item, end =',')

Sample output is

1 2 3 4 5 6 7 8 9 10 49894,25040,12555,6251,3142,1523,787,392,202,111,49,21,10,10,6,2,3,0,1,0,0,1,0,0,0,0,0,...

the remaining all zero...

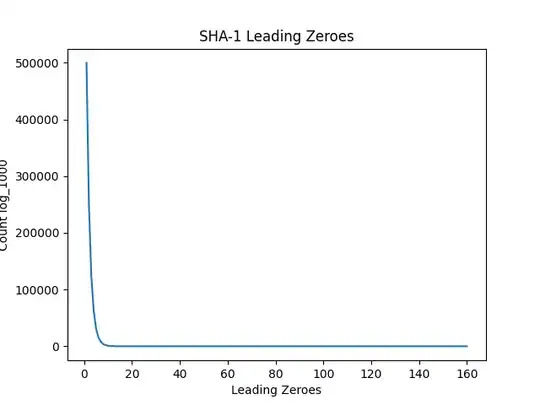
The graph of the event.

Note that it is possible to draw this together with $n/2^i$, however, they are so close to each other that one needs to zoom.

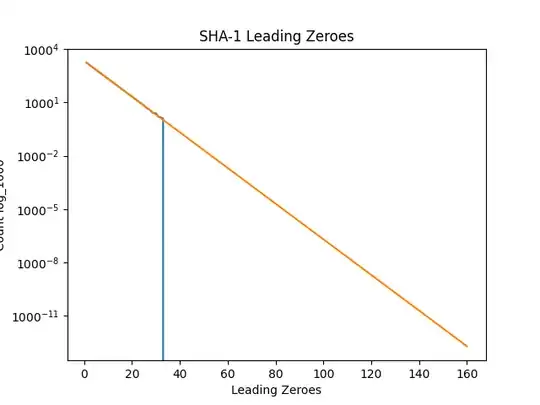
The below is the $\log_{1000}$ scaled $y$ axis with $10^{10} \approx 32$-bits random trials, 1K times more than above, took around 3 hours. With the result data

4999899716,2500040694,1250025163,625012247,312519435,156242195,78129201,39070485,19532263,9766270,4882962,2438565,1220675,610279,305021,152313,75950,38232,19141,9601,4800,2403,1200,610,305,127,75,32,16,15,4,3,2,0,0,...

This time the with $n/2^i$, which is reddish. Since the event is so small compared to space, most of the values are 0 that is the reason for the drop of blue.

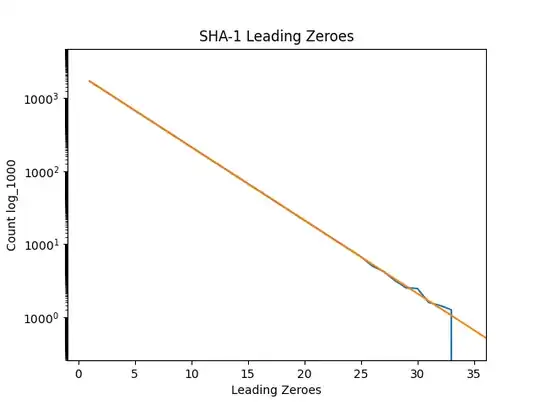
A zoom on the initial part is the below figure.

This tells us that how SHA-1 outputs are close to ideal. We already know that is necessary but not sufficient and the attacks on SHA-1 verifies this.

And, if you replace the SHA-1 with double SHA256 one will see the hardness of mining.

---

Below is the python code that searches and prints for given leading zero.

def searchAndPrint(numberOfTrials,leadingZero):
    for i in range(numberOfTrials): 
        rndValue = random.getrandbits(128).to_bytes(16, 'big')
        hashvalue = hashlib.sha1(rndValue).digest()
    if leadingZero == (160 - int.from_bytes(hashvalue, 'big').bit_length()):
        print(bin(int.from_bytes(rndValue, byteorder='big'))[2:].zfill(128), " ", bin(int.from_bytes(hashvalue, byteorder='big'))[2:].zfill(160))


searchAndPrint(numberOfTrials,2)

---

Plotting part as per request;

def expectedGraphData(space,div2):    
    for idx,item in enumerate(div2) : 
        div2[idx] = space /pow(2,idx+1)
def plotTheGraph(a_list, leading,div2):
    plt.plot(a_list,leading)
    plt.plot(a_list,div2)
    plt.title('SHA-1 Leading Zeroes')
    plt.xlabel('Leading Zeroes')
    plt.ylabel('Count log_1000')
    plt.yscale('log',base=1000)
    plt.show()
xAxislist = list(range(1, 161))
expectedValues   = [0] * 160
expectedGraphData(numberOfTrials,expectedValues)
plotTheGraph(xAxislist,leadingZeros, expectedValues)

Answer 3

just bruteforce it; one possible way to do it in PHP would be:

... i'm not sure which way to count the bits, code to count them in both directions follows:

---

<?php
declare(strict_types = 1);
$bit1_flag = 1 << 7;
$bit2_flag = 1 << 6;
// (and i know the fugly for loop should be a do{}while() instead, anyone feel free to fix it, idc)
for ($i = 0; $i < PHP_INT_MAX; ++ $i) {
    $str = (string) $i;
    $hash = hash("sha1", $str, true);
    $ord = ord($hash[0]);
    if (($ord & $bit1_flag) || ($ord & $bit2_flag)) {
        continue;
    }
    break;
}
function strtobits(string $str): string
{
    $ret = "";
    for ($i = 0; $i < strlen($str); ++ $i) {
        $ord = ord($str[$i]);
        for ($bitnum = 7; $bitnum >= 0; -- $bitnum) {
            if ($ord & (1 << $bitnum)) {
                $ret .= "1";
            } else {
                $ret .= "0";
            }
        }
    }
    return $ret;
}
var_dump($str, strtobits($hash), bin2hex($hash));

which prints

string(1) "1"
string(160) "0011010101101010000110010010101101111001000100111011000001001100010101000101011101001101000110001100001010001101010001101110011000111001010101000010100010101011"
string(40) "356a192b7913b04c54574d18c28d46e6395428ab"

it seems SHA1("1") starts with 2x zero bits

---

-OR- alternative code counting bits in the other direction...:

---

<?php
<span class="math-container">$bit1_flag= 1 &lt;&lt; 0;
$</span>bit2_flag= 1 &lt;&lt; 1;
// (and i know the fugly for loop should be a do{}while() instead, anyone feel free to fix it, idc)
for(<span class="math-container">$i=0;$</span>i&lt;PHP_INT_MAX;++<span class="math-container">$i){
    $str=(string)$i;
    $hash=hash("sha1",$str,true);
    $ord=ord($hash[0]);
    if(($ord &amp; $bit1_flag) || ($ord &amp; $</span>bit2_flag)){
        continue;
    }
    break;
}

function strtobits(string <span class="math-container">$str):string{
    $ret="";
    for($i=0;$i&lt;strlen($str);++$i){
        $ord=ord($str[$i]);
        for($bitnum=0;$bitnum&lt;8;++$bitnum){
            if($ord &amp; (1&lt;&lt;$bitnum)){
                $ret.="1";
            }else{
                $ret.="0";
            }
        }
    }
    return $ret;
}
var_dump($</span>str,strtobits(<span class="math-container">$hash),bin2hex($</span>hash));

which prints

string(1) "5"
string(160) "0011010100101100000111100110101101011001001111001000000101011111010001100110011111110000001110100110110001101001011010000101101001110010011110100101011000100011"
string(40) "ac3478d69a3c81fa62e60f5c3696165a4e5e6ac4"

it seems sha1("5") starts with 2x zero bits