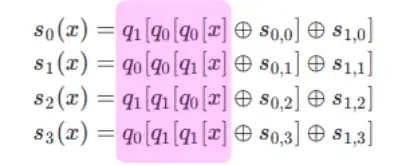How does Twofish avoid weak keys if it uses key-dependent S-boxes?

Question

From section 7.2.2 of the Twofish paper, the four S-boxes for the 128-bit cipher are generated with:

$$\begin{align} s_0(x) &= q_1[q_0[q_0[x] \oplus s_{0,0}] \oplus s_{1,0}]\\ s_1(x) &= q_0[q_0[q_1[x] \oplus s_{0,1}] \oplus s_{1,1}]\\ s_2(x) &= q_1[q_1[q_0[x] \oplus s_{0,2}] \oplus s_{1,2}]\\ s_3(x) &= q_0[q_1[q_1[x] \oplus s_{0,3}] \oplus s_{1,3}] \end{align}$$

Here, $q_0$ and $q_1$ are fixed 8-bit permutations, and $s_{i,j}$ are bytes derived from the keys indirectly via a Reed–Solomon matrix. They claim that this scheme does not produce any weak S-boxes:

Few or no keys may cause the S-boxes used to be “weak,” in the sense of having high-probability differential or linear characteristics, or in the sense of having a very simple algebraic representation

Why is this? How can Twofish avoid weak keys while using key-dependent S-boxes?

Answer 1

The key to the answer lies within these two snippets:-

These results help confirm our belief that, from a statistical standpoint, the Twofish S-box sets behave largely like a randomly chosen set of permutations.

and

There should be few or no pairs of keys that define the same S-boxes. That is, changing even one bit of the key used to define an Sbox should always lead to a different S-box. In fact, these pairs of keys should lead to extremely different S-boxes.

Taken together, they describe an quasi encryption/hash of the key à la SEAL (but simpler). Perhaps akin to a CRC calculation or a mini randomness extractor. Even prior to the MDS matrix. There's probably a better scientific term for it.

$q_0$ and $q_1$ are fairly good S boxes themselves. Even though they are random permutations, their arrangement has been numerically optimised for differential and linear characteristics of $ \frac{10}{256} $ and $ \frac{1}{16} $ respectively, and no more than two fixed points. Taken with the permuted arrangement in the three levels deep nested look ups of $q_0$ and $q_1$ within the definition of $S_i$, it's extremely unlikely that you'd find pre-images that create all weak $S_i$. It's difficult to algebraically define what a related key might look like for a given pre-image. That's just a consequence of all nested look ups into random permutations. The permuted nesting is highlighted below:-

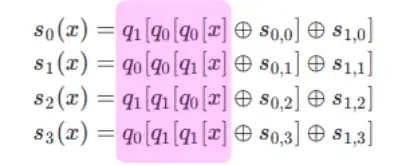
Like you, the authors worried about weak keys too. Hence a large § 7.2.3 Exhaustive and Statistical Analysis. Monte Carlo simulation seems to confirm their assumptions that weak keys are quite unlikely due to the pseudo permutation and avalanche behaviours. Your "very simple algebraic representation" doesn't occur due to the inherent randomness within $q_i$, where the shortest computational representation of $q_i$ is $q_i$.