I have not found a specific answer to this question on here.
Shor's algorithm can be used to factorize a large (semi)prime $N$ by reducing the task to period-finding of a function $f(x)=x^a$ mod $N$.
This is done by creating an equal superposition over all pairs of $a_i$ and $f(x)=x^{a_i}$ for a random $x$, then measuring $f(x)$ causing the superposition to collapse into all $a_i$ for which $f(x)$ is our measures value. Using "Fourier sampling" (I have not fully understood this part) we can then obtain the period of $\ f$ and with .5 probability this yields a non-trivial square root of $N$ which leads to a prime factor.
(Plase correct me if my understanding of the above is flawed)
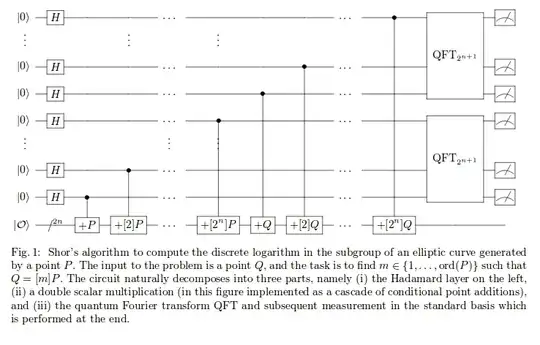
Now how can this algorithm be applied to Elliptic Curve schemes like ECDSA? I struggle to find an explanation for how the discrete log problem for groups over elliptic curves could be solved using Shor's.
EDIT: I would just as well appreciate a reference to other papers except Shor's, that explain the case of Shor's algorithm on DLPs.