Increasing the brute force search time by repeatedly using an an all-or-nothing transform as padding

Question

I'll explain some extra steps I'd like add to the example given in this document, to further slow down each brute force key attempt, and then you guys can tell me why it wouldn't work.

As an example, if I send you a eight-megabyte message encrypted in all-or-nothing CBC mode with a 40-bit DES key, the adversary must decrypt the entire eight-megabyte file in order to test a single candidate 40-bit key. This expands the work-factor by a factor of one-million, compared to breaking ordinary CBC mode. Since one million is approximately 2^20, to the adversary this feels like having to break a 60-bit key instead of a 40-bit key!

The terminology:
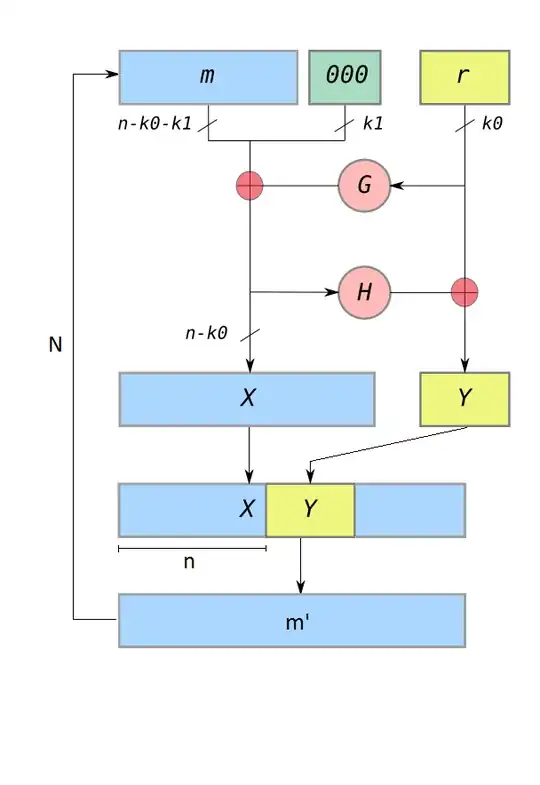
AONT = the all-or-nothing transform like OAEP (where I stole the names)
m = message
r = random number
G and H = some cryptographic hash functions
X = m ⊕ G(r)
Y = r ⊕ H(X)
N = random number, or 10
n = random number between 0 and B'
key1 = regular encryption key (40-bit)
B = number of message blocks
m' = X with Y beginning at a random block instead of being appended to the end
B' = number of message blocks in m'

N is to decide how many times you want to pad the message, between 10 and the largest number of blocks you would want to add, it could be weighted to usually give smaller values (but could sometimes larger values).

To encrypt::
have m, key1, and generate N
perform an AONT on m
insert the new block at a new random position n
repeat the last two steps N times (using m' instead of m)
apply the encryption to the pseudo-message m'
securely send key1
send the encrypted message

To decrypt::
have the encrypted message, key1
decrypt using key1
sequentially pull out and try each block (each location 0 to B') as Y
reverse the AONT
for each possible new pseudo-message, sequentially pull out and try each block (each location 0 to B'- N) as Y
reverse the AONT
...
repeat these steps until the message is recognized

To brute force::
pick a key from the keyspace to try
decrypt using the key
sequentially pull out and try each block (each location 0 to B') as Y
reverse the AONT
for each possible new pseudo-message, sequentially pull out and try each block (each location 0 to B'- N) as Y
reverse the AONT
...
(wrong key) repeat until no more blocks
(right key) repeat until the message is recognized

If you used this method to pad all messages to some fixed size, and some were short( keys, emoticons) and others were long (images, datasets) then an attacker would have to process each attempt down to the last block.

This way the brute force and decrypt methods have to perform the AONT B'! times for each key (increases factorially with the size of the message). But even if the size N is fixed at 10 this is still a big number for 8 megabytes as N!-(N-10)! is large for N = 500000.

Instead of having the decrpyt method guess each start location of the Y block you could send key2 that is a seed for a CSPRNG. It would generate numbers until greater than B, then wrap around to find the location of the Y block to pull out, repeat N times. But I don't know if this is then a big increase, or if its just an x-bit key + an x-bit key (which might only take a bit longer than a x+1 bit key).

Answer 1

I think your problem lies here:

and then you guys can tell me why it wouldn't work.

Cryptography is NOT about "i'll just throw it here because WHY NOT". Cryptography is about "Why I should throw that here". We don't add random things to "maybe make it secure", but instead we focus on solving problems that aren't solved.

This is precisely why your questions are considered questionable. You try to fix something that isn't broken.

Let's assume that there exists a device that can only do X bit cryptography. We have scheme to fix such device already: Perform 3*X work for 2*X bit security.

How it fares against your algorithm?

For start, we have to assume that messages are precisely having some count of bytes. Less than that and we have our key recovered, more than that and our device won't be able to find key in feasible time. That's already terrible, but let's assume we have a device that always just sends 8megabyte message (your example).

Next, we have to assume that our device won't have to decrypt anything because then it has to perform 20bit key breaking itself, when it relies on 40bit security. If it was able to do that, it wouldn't use 40bit key to begin with. We could use CSPRNG as you suggested, but if we have CSPRNG then we can use CSPRNG alone to just implement cipher stream. So your algorithm again will be useless. So let's assume we don't have CSPRNG, and we just encrypt data.

Only if we don't encrypt and have messages of 8megabytes we can have X+20-bit security with your scheme (keys up to 80bits are deemed unsafe). Or we can triple encryption and decryption time for 2*X-bit security. For 40-bit cipher that gives us 80-bit security. We can combine that scheme again to get even more, while with your scheme we would have to change message size.

This is 3rd time you try to push variation of your algorithm, but you never asked yourself "where it would be useful". We already have 3DES to solve DES 56-bit key problem that has far less requirements and gives far better security. If we have CSPRNG we can simply make it into stream cipher. We constantly ask people here to stop "rolling their own", because problems they try to solve were already solved. Instead we ask people to focus on finding solution to their problem. So please take a look at 3DES for how to properly secure short key algorithm. There is not a single reason which makes your algorithm better (memory requirement, time requirement, security given, no-decryption assumptions).

Please also consider that analyzing anything TAKES TIME. We cannot simply watch someone change something in their algorithm without thinking too long and then analyzing it again. We don't have time for that, especially if solution is as simple as "or just use better cipher". That person will be ignored eventually, because nobody will take care to explain for N-th time same things. Please don't do that, we have limited time and variations of "let's just replace that with that" are nearly endless.