Is CMAC vulnerable to length extension attacks?

Question

Given $m_1, m_2$ such that $MAC_k(m_1) = MAC_k(m_2)$ is it possible to construct more collisions with pairs of the form $m_1|x, m_2|x$?

Here is the CMAC picture from Wikipedia where it is only part of the one-key MAC article:

I don't see how it could be because it treats the last block of the message differently but this was mentioned in the comments of another question so I wanted to clarify.

Here is the quote from poncho:

CMAC and XCBC are similar to the UMAC case (even though a universal hash is not involved); if you find two messages that have the same CMAC value, it is likely that a simple length-extension to the two messages will allow the attacker to create other pairs of messages with the same MAC.

Bonus question: Are there other ways to exploit a collision?

Answer 1

Given $m_1, m_2$ such that $MAC_k(m_1) = MAC_k(m_2)$ is it possible to construct more collisions with pairs of the form $m_1|x, m_2|x$?

Yes, given two restrictions:

• $MAC_k$ is not truncated (e.g. if it is based on AES, then the tag is 128 bits long). This observation does not apply on a collision on (for example) truncated 64 bit tags (assuming that the bits deleted during the truncation don't also happen to collide).

• $m_1$ and $m_2$ are either both a multiple of the block size in length, or alternatively both not a multiple of the block size in length. For example, if we assume AES, then it works if $m_1, m_2$ are $32, 48$ bytes in length (both multiples of 16), and if they are $23, 31$ bytes in length (neither multiples of 16), but not if they are $16, 17$ bytes in length.

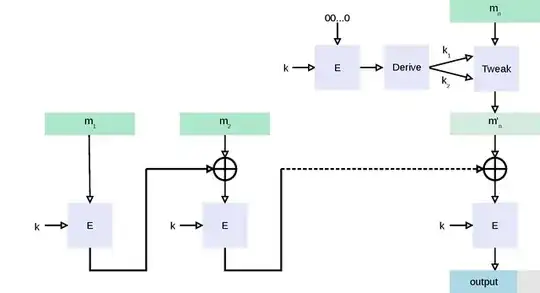
Here is how CMAC works (at the end of the message, which is where the interesting part it):

• Block $n-1$ is processed, generating an internal chaining value $I_{n-1} = E_k( m_{n-1} \oplus I_{n-2})$

• the last block is processed; the block is zero padded (if not full), one of $k_1, k_2$ is selected (depending on whether the block is full), and we do a final computation $tag = E_k( m_i \oplus k_{1,2} \oplus I_{n-1})$

Now, we assume a full block collision, that is, $tag = tag'$. Using the above definition, we have:

$$E_k( m_n \oplus k_{1,2} \oplus I_{n-1}) = E_k( m'_n \oplus k_{1,2} \oplus I'_{n-1})$$

Removing the encryption, and noting that both sides select the same $k_1, k_2$ value, we can simplify this to:

$$m_i \oplus I_{n-1} = m'_i \oplus I'_{n-1}$$

Now, we can consider what would mapping if we compute the CMAC of the values $m || padding || x$, $m' || padding' || x$ (where $x$ is an arbitrary bits string, and where $padding, padding'$ are the zero pad to bring $m, m'$ to a multiple of block size in length; they are zero length if $m, m'$ is already a multiple of block size).

In this case, at step $n$, the two sides will compute:

$$I_n = E_k(m_n \oplus I_{n-1})$$ $$I'_n = E_k( m'_n \oplus I'_{n-1})$$

These two values are the same; the rest of the CMAC computation depends only on $x$ (which is the same on both sides), and so will result in the same tag; hence giving us another collision.