Exploiting AES with IV similar to password and fixed key

Question

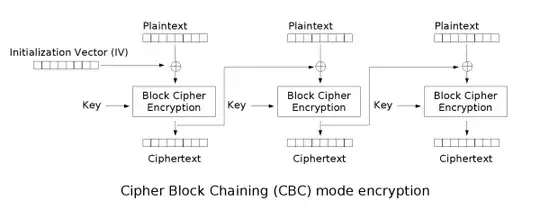
While reviewing a 'secure communication protocol' made by a colleague, I noticed a usage of AES-128 CBC that caught my eye. I think they are trying to implement a HMAC but have made some very questionable decisions.

The steps look like this:

1. The IV is initialized to be the same as a user's (plaintext) password with just one byte changed.
2. AES CBC takes the password, this IV, and a key as input, however the same key is used each time.
3. The output of this encryption is then XORed with the original password, giving the user's password hash.

Now presuming I have the key and some hashed passwords, is it possible to obtain the original plaintext passwords, in order to prove to my colleague that this system is horribly broken?

Answer 1

It seems completely possible to break this scheme. Lets take 2 passwords, using some deterministic padding scheme. Now remember that the IV is XOR'ed with the plaintext before encryption:

Now it seems that the output of this XOR operation will only be different by one byte. So if you have enough passwords that are hashed then the input and therefore output of the blockcipher is likely to repeat. Due to the birthday bound repetition is likely with a chance of 0.5 after 16 tries.

One way to take advantage of this as attacker is to create a few accounts with different passwords. The output of the cipher can be retrieved using the output of the password hash, recovered later. It can simply XOR this value with the password given, which will result in the output of the cipher. Then the attacker can XOR this value with the other password hashes until it finds something that looks like a valid password strings (e.g. by detecting if there are no control characters in the output). This way most if not all passwords should be retrievable.

The fun thing with this attack is that you don't even need the key. The adversary just requires a hashing oracle (the server itself) and (parts of the) hash database.