Is there a floating point CSPRNG?

Question

Is there a floating-point CSPRNG that operates, natively, using floating point operations?

Looking for a CSPRNG that's very fast on GPUs, and would be hard for a CPU to beat.

EDIT: Floating point doesn't matter too much. Specifically, I'm looking for something for which GPUs or FPUs are, by far, the optimal hardware to use: as opposed to custom hardware, because the operations used are already heavily optimized on GPU.

My understanding is that floating-point-operations (FLOPS) are probably the best candidate here. (It seems to me that most chaotic attractors can be trivially run using FLOPS.)

Answer 1

Are you sure?

Float operations are very hard to reproduce in diverse environments.

Do you round towards positive, negative or zero? Do you handle denormals or just treat them as zero? What about dividing by zero?

I'm sure we would love to have that problem with every cipher we implement.

Looking for a CSPRNG that's very fast on GPUs, and would be hard for a CPU or FPGA to beat.

To beat FPGA... don't do anything. There are problems that are slow on CPUs & GPUs, but otherwise you won't have as big FPGA that can reach nearly same frequency. If that wasn't case we wouldn't have processors, just builtin FPGAs that switch between GPUs and CPUs...

To beat CPU... just use something that uses a lot of simple math... +,-,xor,ror,rol etc. This doesn't have to be on floats, ints will suffice. Chacha20 might work well on GPUs. Note that this won't be slow on CPUs, it will just be faster on GPUs because it parallelizes well (and this is always case, because CPUs are complex beasts that can do more than GPU, except there just isn't enough of it for raw number crunching at that speed).

Honestly, most cryptographic primitives will be faster on GPUs because they frequently rely on number crunching, and rarely do any significant memory access and/or branching.

Just remember that there are still ASICs that will always win against you, because they are exceptionally good at number crunching (and if you are looking to outrun them, argon2 and CPU are your friends).

Answer 2

Here is an example of what I'm looking for. Yes, it hasn't been tested. The underlying attractor has been proven a good source of randomness, and approximations of this technique have been used for other CSPRNG systems.

• Convert a seed to 4 FP numbers between 0 and 1.

• Calculate the hyperlorenz attractor using FP arithmetic for N iterations, and these numbers as the initial conditions.

• For reference on why I would choose something like this: https://www.researchgate.net/publication/308109900_Image_Encryption_using_Four-Dimensional_Hyper_Chaotic_Lorenz_System

• Take the last X FP outputs, hash them with SHA3, then take the result and call it your first random number. Continue iterating N times and outputting the results.

While the hashes are fast, the FP operations will be slow. So this will, slowly, generate pseudorandom numbers, and will be both FP heavy, with highly sequential FLOPs.

• To prevent cryptanalysis, the settings for N and X must be high enough that you're not capturing too many bits per iteration. Keeping X low increases the ratio of FLOPS. Keeping N low makes the algorithm more efficient, but less secure.

EDIT: Although the lorenz family of attractors are provably unpredictable and well-studied, the number of bits to capture per iteration is a matter that would require some experimentation and analysis to be provably secure. Possibly it could be a number much less than one. In which case this could be terribly inefficient. There are other attractors used in secure cryptographic pseudo random number generators that may yield a better entropy level per iteration.

(I suspect that a fun paper to write would be one that can turn any chaotic attractor into a CSPRNG by determining optimal values of X and N for a given level of security required, level of leakage, etc. Autotune for CSPRNG.)

The concern responders have for the approximations used in FP operations aren't really an issue and are basically useless non-information, please stop posting them. Far more data is discarded and approximations made in other attractor-based integer CSPRNGs. In fact you could simply change any FP system into an integer system with sufficient motivation. But the point would be to make a system that's optimized for FPU's... which are can be analogized as the cheapest, most powerful and plentiful ASICs on earth.

Answer 3

No. There are no common floating point PRNGs.

If you search the literature there are few PRNG that utilises native floating point computation. This not so cunning program illustrates why they are unreliable across different architectures. Try the following on i386 stuff:-

for ($i=0; $i<1000; $i=$i+0.1) {}
print "$i";

The answer is:-

1000.00000000016

The (unexpected) extra 16 part at the end is rounding due to the inability to accurately represent decimal numbers in binary. And this rounding is highly dependant on the underlying hardware /software.

Repeating with:-

i=0
while i<1000:
    i=i+0.1
print(i)

I get:-

1000.0000000001588

Where's the 16 bit gone as I added up exactly the same numbers, this time using Python rather than Perl? And on Atmel, the answer is a round 1000.00. A CSPRNG is validated against an output run of mega bytes of data. With such unpredictable rounding errors, it would be difficult to validate on various platforms. As a relevant aside, it's why computer currency calculations are performed as integers.

Another unexpected issue with floating point is that bit wise adjacent numbers aren't the same numerical distance apart. One single adjacent bit change can alter a floating point number by a difference that can vary by an astonishing 24 orders of magnitude. This is better represented with picture like so:-

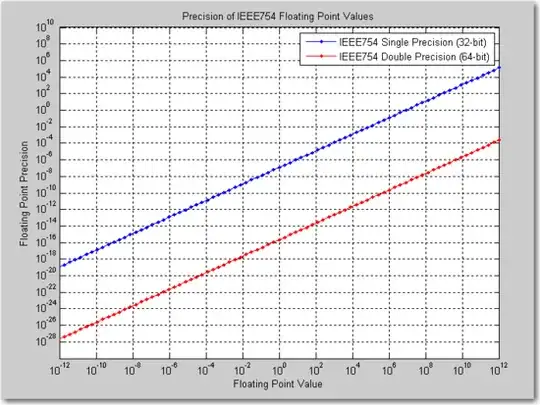
Generators like RC4 and ISAAC (to name two) are entirely based around array indirection functions, and array indices have no meaning unless they're integers. Commonly used left and right bit manipulations also become meaningless on a floating point number as the exponents would break storage conventions.

Of course you can always roll your own thing that will produce random looking output. So a construction using a hash of the output of my example would produce a cryptographic ally irreversible number stream. So you'd have:-

Hash(Perl program output).

However, the rounding error will bite you as it will form a deterministic (for your specific machine) error bias. So the number stream will be useless for all but the most trivial of applications. So speed is kinda irrelevant. There aren't any CSPRNGs out there.