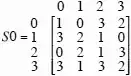I am trying to derive equations for s and t in the cryptanalysis of a Simple DES algorithm, but I haven't been able to deduce it. I have attached an image of the portion that I'm referring to, and I would appreciate it if someone could explain as to how the equations q and r are derived and what would be the derivation for s and t.
The question is actually about Simplified DES (rather than Simple DES as stated), which is an extremely simplified mock-up of Single DES.
From reading the definition of S-DES in the reference used in the question, we get that:
The S-boxes operate as follows. The first and fourth input bits are treated as a 2-bit number that specify a row of the S-box, and the second and third input bits specify a column of the Sbox. The entry in that row and column, in base 2, is the 2-bit output.
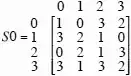
Now let $a b c d$ be the input bits, $q r$ the output bits, use big-endian convention, and reformat that table as:
abcd qr abcd qr abcd qr abcd qr
0000 01 0010 00 0100 11 0110 10
0001 11 0011 10 0101 01 0111 00
1000 00 1010 10 1100 01 1110 11
1001 11 1011 01 1101 11 1111 10
In order to verify the equations $q=abcd\oplus ab\oplus ac\oplus b\oplus d$ and $r=abcd\oplus abd\oplus ab\oplus ac\oplus ad\oplus a\oplus c\oplus 1$, just compute what $q$ and $r$ they give for each of the $2^4$ combinations of input, and compare that to the reformatted table; this is left as an exercise to the reader.
There is no systematic practical method to derive the most compact equation for a sizable bit table, and in the case of DES S-boxes this has been the subject of intense research. One systematic method leading to the most compact representation of an arbitrary boolean function as OR-of-AND-terms is known as Karnaugh map, but here the equations are wanted as XOR-of-AND-terms, and I know no analogous method. With 4 entries, finding the shortest equation (by some metric) that match would be tractable by brute force with a computer.
Still, here is how one of the equation could have been derived by hand. First we rewrite the table with the arguments in Gray order
a | 0000000011111111
b | 0000111111110000
c | 0011110000111100
d | 0110011001100110
--|-----------------
q | 0110100101111010
r | 1100110001011110
By comparing the line for $d$ with the line for $q$, it is striking that a bit flip of $d$ cause a flip in $q$, except when $a=b=c=1$; in other words, $q'=q\oplus d\oplus abcd$ is independent of $d$. We have reduced the problem to finding an equation for $q'$, with table
a | 00001111
b | 00111100
c | 01100110
--|---------
q'| 00110110
and some trial and error is enough to find $q'=ab\oplus ac\oplus b$, from which $q=abcd\oplus ab\oplus ac\oplus b\oplus d$ follows.
A Karnaugh map is definitely the way to go to understand the concept and derive the equations in a few binary variables.
If you want to do this for a larger numbers of variables, look into Quine-McCluskey. There's a sizable introductory literature in logic design that is relevant to this.
In general, since algebraic cryptanalysis involves doing a lot of algebraic normal form to conjunctive normal form (and vice-versa), it might be worth writing some kind of converter, or using one that is already available (e.g. Mathematica, SAGE).
