Should HMAC-SHA3 be preferred over H(C(k,M))?

Question

If I understand correctly SHA-3 (Keccak) is resistant against more attacks than SHA-2. This would make it possible - again if I understand correctly - to use SHA-3 with a simpler scheme than HMAC.

Would there still be a reason to use the HMAC construction with SHA-3? Would it be a better idea to simply use $H(C(k, M))$ where $H$ is simply SHA-3 and $C$ is a function to create a canonical representation (encoding) of the key $k$ and the message $M$ to set them apart?

Of course I imagine that HMAC-SHA3 will be used in the majority of protocols anyway as SHA-3 was created as a drop in replacement of SHA-2. But is there any security related reason to use HMAC-SHA3 over an (even) simpler scheme?

Answer 1

HMAC does not provide an obvious security improvement over the KMAC construction, which is optimal for Keccak based functions. HMAC is designed to create a secret initialization vector or IV for Merkle-Damgård type hash functions, KMAC does the same for sponge based hash functions but much more efficiently. HMAC also needs to deal with the length extension property

KMAC extends the key to the block size and prepends it to the message. I believe this will be standardized (if it has not already) as the default MAC construction for SHA-3. Because it extends the key to the block size, an F iteration is performed over the key prior to message absorption, creating a secret keyed state.

This is the basic sponge MAC construction discussed during the Keccak design phase, and in later discussion of both Keccak and SHA-3. There needs to be some kind of encoding or padding to effectively separate keys of different sizes, but this is not discussed in those documents; the $C$ function you mention would perform such separation. KMAC as discussed during the August 2014 SHA-3 workshop shortly after the publication of FIPS 202 uses the "keypack" function to pad the key and encode the byte-length of the key block as an 8-bit value, using a minimum of 9 additional bits beyond the length of the key: $\operatorname{Keypack}(K, l) = \operatorname{enc}(l /8) | K | 1 0 ^{l-\operatorname{len}(K)-9}$ where $l$ is the block size.

The "block size" of SHA-3 is at least 576 bits for all variants, meaning a 512-bit key can key the state with only one additional iteration of $f$. Additionally, since there is no block or bit counters, a device with low computational resources but enough memory can simply keep the keyed state as its default state for MAC computations and suffer no performance hit when compared to plain hashing.

Update: Since this answer was originally written, NIST has published SP 800-185 standardizing KMAC and a few other useful Keccak-derived constructions.

Answer 2

You're essentially asking if SHA-3 can use a keyed hash instead of an HMAC.

The short answer is yes. But there's more to it than that.

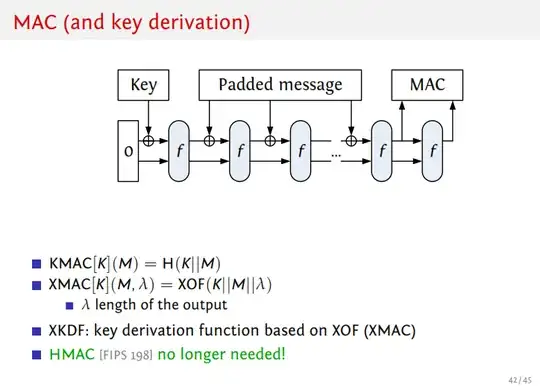
In the SHA-3 competition, two of the finalists (Keccak and Skein) were specifically designed to have a one-pass MAC as part of their design, and that's what the answer above is giving about Keccak. KMAC is Keccak's one-pass MAC. Skein also has a one-pass MAC. It's a fine answer — really, you ought to use KMAC rather than either a keyed hash or HMAC because KMAC has security proofs over a keyed hash and it's faster than HMAC. But that isn't the question you asked, you asked about keyed hashes.

But any of the five finalists are collision resistant enough that a keyed hash is likely to be as good as HMAC. In that word "likely" is presuming that they're as collision-resistant as presently thought. HMAC is a construction that protects against certain types of flaws in a hash function, but what that actually means is a huge discussion that you didn't ask about.

If you're going to do a keyed hash function, you should hash . I am presuming that your message has been canonicalized in whatever way you want. You want to hash the key before the message and the length of each field before the field because assuming hash flaws (like those that exist in Merkle-Damgård constructions), that puts the important things where they're less vulnerable to collision issues, and collisions are much harder.

The bottom line is that if you're going to use SHA-3, you should use KMAC. If you're using an HMAC, yes, you can drop-in-replace an older function with SHA-3 and that's even better. And yes, if you use a modern hash function like any of the SHA-3 finalists with a keyed hash, it can be as good as either.

— Jon (Skein co-author)