DES hardware implementation of substitution lookup table [ ReWorked ]

Question

I'm a crypto enthusiastic and student of cryptography. I'm developing a project with other students titled "A hardware implementation of a DES cryptography for educational purposes", our idea was to make a simple version of DES encryption in a piece of hardware to help students that are learning cryptography understand better how this complex encryption method is implemented in hardware.

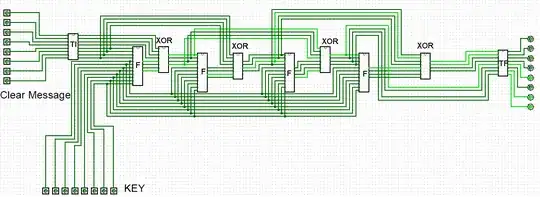
First, we started the system with an input of 8 bits to simplify the complexity and save space. Them, we created all the parts of DES cryptosystem (Initial Permutation, Feistel, XOR, Final Permutation).

Here is a image of our main system:

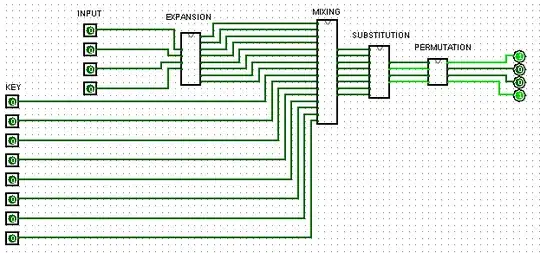
One of the important parts of the system is the Feistel Function. The Feistel part were divided in 4 parts, Expansion, Mixing, Substitution, Permutation. Each of these parts are implemented as following:

The expansion CI just take the bits and duplicate them putting the new bit in the adjacent output, this CI receive 4 bits of the right part of the input and outputs 8 bits. Mixing just take the first bit of the output of expansion and XOR with the first bit of the key(8 bits) and so on... the output is 8 bits. Now we have the most important part and the part that I personally think we're missing something. The Substitution in witch is the S-Box, this CI has an 8 bits input and these 8 bits are divided in two parts(because we developed only 4 bits S-Boxes) these parts enter the S-Box and the S-Box output is of 2 bits, when you see the S-boxes of DES, all of them uses a lookup table, we've the idea of using the Karnaught map for implementing this table.

Our table :

And here is where we stopped, because we implemented all of this and had fail results like this:

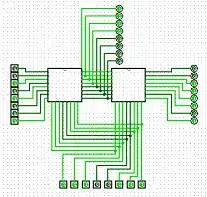
The S-Box works like a lookup table on software but the system does not work, is there any specific way that these look up tables are created ? We couldn't see any pattern in the outputs of the table, do you guys have any material to help us ? I feel like this is the last thing to work on.

Thank you for reading it all. Please leave a comment! :) Thank you again!

Answer 1

As for "how to build the substitution as hardware", it should be easy if you know any of the hardware description language (eg. VHDL or Verilog). Simply write the Sboxes of DES, then the synthesis software will handle the rest. You can also "synthesis" by hand, although that may take a lot of effect.

Still, I'm not sure if this is what you are looking for. Your post says "thought of a very simple DES circuit of 8 bits". It looks like you have designed a simplified version of DES for teaching. However, your post didn't give the description of your simplified DES; only provided some implementation schemes. If you have altered the Sbox of DES to 8-4 (like your picture above), then implement it like that is fine?

Answer 2

A simple way to think of the S-boxes of DES when it comes to a hardware implementation is: 8 independent ROM ICs, each with 6 address input lines and 4 data out lines. In an educational physical implementation with retro standard ICs, two such ROMs fit a 4 kiB EPROM (a 2732). Some actual software implementations of DES do group S-boxes two by two in order to reduce the number of table lookups.

Another way is: 8 times, 4 independent boolean functions of the same 6 input bits; for a total of 32 independent boolean functions of 6 input bits out of 48 input bits (which themselves come from the key, with a wiring dependent on the round and if we are enciphering or deciphering). It is well known how to build any boolean function of 6 input bits (e.g. using Karnaugh maps), hence in principle build these 32 boolean functions. However Karnaugh maps do not yield efficient/compact circuits in the case of DES S-boxes.

There is little exploitable regularity in the DES S-box functions. The most striking one is that each line of numbers of the spec of the S-box values (FIPS 46-3 appendix 1) is a permutation of $\{0\dots15\}$. It follows that we can model each of the 32 boolean functions by: 4 functions of 4 input bits (coding columns on that spec) set for precisely 8 out of 16 combination of these 4 inputs, followed by selection of the appropriate of the 4 results of these 4 functions according to 2 other input bits (coding line in the S-box). This translates into a trivial systematic construction of the functions using NAND gates with at most 8 inputs, of depth 3 (including input inverters) plus the final 1-out-of-4 multiplexer stage. Using this structure, it is very easy to fit two S-boxes in a generic PAL with 12 inputs plus internal feedback and 10 outputs, at least 8 of which having at least 8 input terms. The once-popular PALCE22V10 is ample.

The problem of minimizing the complexity of these 32 functions, including considering that they are evaluated together and some work can be shared among the 4 functions belonging to the same S-box, has been extensively studied; for example by Matthew Kwan: Reducing the Gate Count of Bitslice DES, 2000, eprint 2000/051; however he is focusing on 2-input gates and considers XOR of unity cost, which is fine for software, but hardware has different constraints.