What are options to compute DES retail MAC (aka ISO 9797-1 mode 3) under PKCS#11?

Question

The DES retail MAC, also known as ISO 9797-1 mode 3 with DES, computes the MAC of a block of data using a 16-byte (112 bit) key. It can be seen as CBC-MAC using simple DES with the first half of the key for all the blocks, except the last where 3DES with the full key is used. I've left padding and truncation out of the picture.

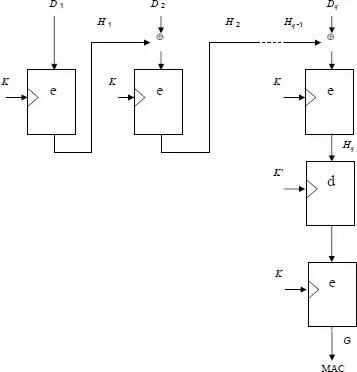
I need to compute that MAC

• using a standard PKCS#11 token,
• with all DES operations in the token (for fear of side-channel attacks),
• using PKCS#11 semantic compatible with most tokens,
• if at all possible, with built-in derivation of the key using CKM_SHA256_KEY_DERIVATION (the key is the first 16 bytes of the hash) and no exposition of that key material in the host's RAM.

Is that DES retail MAC sometime available in PKCS#11, under some name that I missed? If not (or that's not supported in my token), what are my options to implement that MAC given that the token I use is documented as supporting encryption using CKM_DES3_CBC, but not CKM_DES_CBC (deprecated), nor MAC using CKM_DES_MAC, CKM_DES3_MAC (not available)?

So far the best I see is two separate encryptions using CKM_DES3_CBC, the first with a DES2 key emulating a DES one; but that's hairy, and I fail to derive the first key inside the HSM.

Answer 1

An answer surfaced from careful reading of appropriate documentation.

The MAC in the question is also defined in ANSI X9.19, and is supported by some PKCS#11 tokens as the mechanism CKM_DES3_X919_MAC_GENERAL.

Other than that, this MAC can be simulated using CKM_DES_MAC_GENERAL (or CKM_DES_CBC or CKM_DES3_CBC) for all but the last block, then CKM_DES3_CBC; but derivation of the key for the first part is hairy, and an adversary observing the intermediary result for a single plaintext can mount a key recovery attack requiring about $2^{56}$ work.

Independent of implementation and intermediary result, as pointed by poncho in comment, there is a key recovery attack on that MAC when so much plaintext is processed that an internal collision occurs, which is in the order of $2^{32}$ MACs, then allowing an attack with about $2^{57}$ work.